题目内容
选修4-5:不等式选讲已知关于x的不等式|ax-1|+|ax-a|≥1(a>0).
(1)当a=1时,求此不等式的解集;
(2)若此不等式的解集为R,求实数a的取值范围.
【答案】分析:(1)当a=1时,可得2|x-1|≥1,即 ,由此求得不等式的解集.
,由此求得不等式的解集.
(2)不等式|ax-1|+|ax-a|≥1解集为R,等价于|a-1|≥1,由此求得实数a的取值范围.
解答:解:(1)当a=1时,可得2|x-1|≥1,即 ,解得
,解得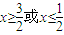 ,
,
∴不等式的解集为 . …(5分)
. …(5分)
(2)∵|ax-1|+|ax-a|≥|a-1|,不等式|ax-1|+|ax-a|≥1解集为R,等价于|a-1|≥1.
解得a≥2,或a≤0. 又∵a>0,∴a≥2.
∴实数a的取值范围为[2,+∞). …(10分)
点评:本题主要考查绝对值的意义,绝对值不等式的解法,体现了等价转化的数学思想,属于中档题.
 ,由此求得不等式的解集.
,由此求得不等式的解集.(2)不等式|ax-1|+|ax-a|≥1解集为R,等价于|a-1|≥1,由此求得实数a的取值范围.
解答:解:(1)当a=1时,可得2|x-1|≥1,即
 ,解得
,解得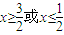 ,
,∴不等式的解集为
 . …(5分)
. …(5分)(2)∵|ax-1|+|ax-a|≥|a-1|,不等式|ax-1|+|ax-a|≥1解集为R,等价于|a-1|≥1.
解得a≥2,或a≤0. 又∵a>0,∴a≥2.
∴实数a的取值范围为[2,+∞). …(10分)
点评:本题主要考查绝对值的意义,绝对值不等式的解法,体现了等价转化的数学思想,属于中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目