题目内容
求焦点在坐标轴上,且经过点A( ,-2)和B(-2
,-2)和B(-2 ,
, )两点的双曲线的标准方程.
)两点的双曲线的标准方程.
【答案】分析:设双曲线方程为:mx2-ny2=1,(mn>0),结合点A(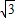 ,-2)和B(-2
,-2)和B(-2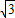 ,
,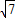 )在双曲线上,可得关于m与n的方程组,求出m与n的值即可得到答案.
)在双曲线上,可得关于m与n的方程组,求出m与n的值即可得到答案.
解答:解:设所求双曲线方程为:mx2-ny2=1,(mn>0),
因为点A(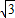 ,-2)和B(-2
,-2)和B(-2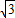 ,
,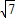 )在双曲线上,
)在双曲线上,
所以可得: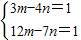 ,
,
解得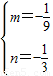 ,
,
故所求双曲线方程为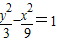 .
.
点评:本题考查用待定系数法求双曲线的标准方程的方法.
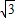 ,-2)和B(-2
,-2)和B(-2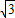 ,
,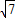 )在双曲线上,可得关于m与n的方程组,求出m与n的值即可得到答案.
)在双曲线上,可得关于m与n的方程组,求出m与n的值即可得到答案.解答:解:设所求双曲线方程为:mx2-ny2=1,(mn>0),
因为点A(
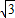 ,-2)和B(-2
,-2)和B(-2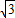 ,
,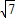 )在双曲线上,
)在双曲线上,所以可得:
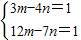 ,
,解得
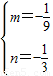 ,
,故所求双曲线方程为
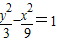 .
.点评:本题考查用待定系数法求双曲线的标准方程的方法.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目