Question

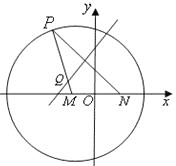
【题目】如图，在四棱锥中，为等边三角形，，，且，，，为中点.

（1）求证：平面平面；

（2）若线段上存在点，使得二面角的大小为，求的值；

（3）在（2）的条件下，求点到平面的距离.

Answer 1

【答案】(1)证明见解析；(2)；(3).

【解析】分析：（1）证明PE⊥AD，PE⊥BE，即可证明PE⊥平面ABCD，从而证明平面PAD⊥平面ABCD；
（2）建立空间直角坐标系，利用坐标表示向量，求出平面EBQ和平面EBC的法向量，由此表示二面角Q-BE-C，求出的值；
（3）利用在平面EBQ法向量上的投影，求出点C到平面QEB的距离．

（1）证明：连接，，

∵是等边三角形，为中点，∴，

又∵，∴，，∴，且，

∴四边形为矩形，∴，，

∴，∴，

又∵，∴平面，

又∵平面，∴平面平面.

（2）如图建系，，，，，，

设，，

∴ ，

设平面的法向量为，

∴，

∴，

平面的法向量不妨设为，

∴，

∴，∴或（舍），

∴.

（3）.