题目内容
20. 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC(1)求证:平面PAB⊥圆O所在平面,
(2)若圆O的半径为2,PA=4,求以圆O为底面,P为顶点的几何体的体积.
分析 (1)由PA=PB,OA=OB,可得OP⊥AB,再利用勾股定理与逆定理可得OP⊥OC,利用线面垂直的判定定理即可证明;
(2)在Rt△OAP中,OP=$\sqrt{A{P}^{2}-A{O}^{2}}$.再利用圆锥体积计算公式可得:以圆O为底面,P为顶点的几何体的体积V=$\frac{1}{3}•π•O{A}^{2}•PO$.
解答 (1)证明:如图所示,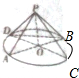
∵PA=PB,OA=OB,
∴OP⊥AB,
∴PA2=OA2+OP2=OC2+OP2=PC2,
∴OP⊥OC,
∵AB∩CD=O,
∴OP⊥平面⊙O所在平面.
(2)解:在Rt△OAP中,OP=$\sqrt{A{P}^{2}-A{O}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
∴以圆O为底面,P为顶点的几何体的体积V=$\frac{1}{3}•π•O{A}^{2}•PO$=$\frac{1}{3}×π×{2}^{2}•2\sqrt{3}$=$\frac{8\sqrt{3}π}{3}$.
点评 本题考查了勾股定理与逆定理、线面垂直的判定定理、圆锥体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.若等差数列{an}的公差d<0,且a1+a11=0,则数列{an}的前n项和Sn取得最大值时的项数n是( )
| A. | 5 | B. | 6 | C. | 5或6 | D. | 6或7 |
8.如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积为( )


| A. | 2 | B. | 6 | C. | 2($\sqrt{2}$+$\sqrt{3}$) | D. | 2($\sqrt{2}$+$\sqrt{3}$)+2 |
 如图,在四棱锥A-BCDE中,AB=AC=$\frac{\sqrt{2}}{2}$BC,点F为矩形BCDE的对角线的交点,G是AE的中点,平面BCDE⊥平面ABC.
如图,在四棱锥A-BCDE中,AB=AC=$\frac{\sqrt{2}}{2}$BC,点F为矩形BCDE的对角线的交点,G是AE的中点,平面BCDE⊥平面ABC.