题目内容
14.已知函数f(x)=$\left\{{\begin{array}{l}{|x-1|}&{(x≤1)}\\{{3^x}}&{(x>1)}\end{array}}$,f(a)=2,则f(f(-1))=9,a=-1.分析 直接利用分段函数利用解方程解a,直接求解函数值即可.
解答 解:函数f(x)=$\left\{{\begin{array}{l}{|x-1|}&{(x≤1)}\\{{3^x}}&{(x>1)}\end{array}}$,f(a)=2,
可得|a-1|=2,解得a=-1,a=3(舍去).
f(f(-1))=f(|-2|)=f(2)=32=9.
故答案为:9;-1.
点评 本题考查分段函数的应用,函数值的求法,考查计算能力.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
19.若数列{an}是首项为1,公比为-$\sqrt{2}$的等比数列,则a4等于( )
| A. | -8 | B. | -2$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
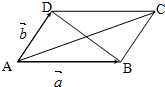 如图在平行四边形ABCD中,M,N分别为DC,BC的中点,已知$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,试用$\overrightarrow a$,$\overrightarrow{b}$表示$\overrightarrow{AC},\overrightarrow{BD},\overrightarrow{AM,}\overrightarrow{AN}$,$\overrightarrow{NM},\overrightarrow{MB}$.
如图在平行四边形ABCD中,M,N分别为DC,BC的中点,已知$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,试用$\overrightarrow a$,$\overrightarrow{b}$表示$\overrightarrow{AC},\overrightarrow{BD},\overrightarrow{AM,}\overrightarrow{AN}$,$\overrightarrow{NM},\overrightarrow{MB}$.