题目内容
6.已知函数f(x)=$\frac{3}{x}$-x+alnx,且x=3是函数f(x)的一个极值点.(1)求a的值;(2)求函数f(x)的单调区间;
(3)设g(x)=f(x)-m,当函数y=g(x)在区间(0,5]上零点的个数为0个,3个时,实数m的取值范围分别为多少?(参考数据:ln5≈1.61,ln3≈1.10)
分析 (1)由f(x)解析式求出导函数解析式,把x=3代入导函数解析式求出a的值即可;
(2)令导函数大于0求出x的范围,即为函数的增区间;令导函数小于0求出x的范围,即为函数的减区间;
(3)令g(x)=f(x)-m=0,得到f(x)=m,可得函数y=g(x)在区间(0,5]上零点的个数是y=f(x),x∈(0,5]与直线y=m交点的个数,根据x的范围,对应导函数的值,以及函数的值,列出表格,即可确定出零点的个数为0个,3个时,实数m的取值范围.
解答 解:(1)f′(x)=-$\frac{3}{{x}^{2}}$-1+$\frac{a}{x}$,
∵x=3是函数f(x)的一个极值点,
∴f′(3)=0,即-$\frac{1}{3}$-1+$\frac{a}{3}$=0,
解得:a=4;
(2)由(1)知f′(x)=-$\frac{3}{{x}^{2}}$-1+$\frac{4}{x}$,
令-$\frac{3}{{x}^{2}}$-1+$\frac{4}{x}$>0,解得:1<x<3,
令-$\frac{3}{{x}^{2}}$-1+$\frac{4}{x}$<0,及x>0,解得:0<x<1或x>3,
则当x∈(1,3)时,y=f(x)单调递增;当x∈(0,1)时,y=f(x)单调递减;当x∈(3,+∞)时,y=f(x)单调递减;
(3)令g(x)=f(x)-m=0,可得f(x)=m,
∴函数y=g(x)在区间(0,5]上零点的个数是y=f(x),x∈(0,5]与直线y=m交点的个数,
由下表:
| x | (0,1) | 1 | (1,3) | 3 | (3,5) | 5 |
| f′(x) | _ | 0 | + | 0 | _ | |
| f(x) | ↘ | 极小值2 | ↗ | 极大值4ln3-2 | ↘ | 4ln5-$\frac{22}{5}$ |
∴函数f(x)在(0,5]的最小值为2,无最大值,
结合大致图象可知:
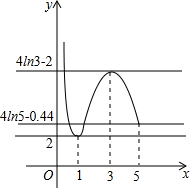
当m<2时,g(x)=f(x)-m的零点个数为0;
当m=2或m>4ln3-2时,g(x)=f(x)-m的零点个数为1;
当2<m<4ln5-$\frac{22}{5}$或m=4ln3-2时,g(x)=f(x)-m的零点个数为2;
当4ln5-$\frac{22}{5}$≤m<4ln3-2时,g(x)=f(x)-m的零点个数为3,
则零点的个数为0个,3个时,实数m的取值范围分别为m<2;2.04≤m<2.2.
点评 此题考查了利用导数研究函数的增减性,以及函数的零点判定定理,利用了数形结合的思想,导函数的性质为:当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N. ,则
,则 ______.
______.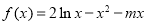 .
. 时,求函数
时,求函数 的最大值;
的最大值; 与
与 轴交于两点
轴交于两点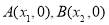 且
且 ,证明:
,证明: .
.