Question

已知实数m>1，定点A（－m，0），B（m，0），S为一动点，点S与A，B两点连线斜率之积为

   （1）求动点S的轨迹C的方程，并指出它是哪一种曲线；

   （2）当时，问t取何值时，直线与曲线C有且只有一个交点？

   （3）在（2）的条件下，证明：直线l上横坐标小于2的点P到点（1，0）的距离与到直线x=2的距离之比的最小值等于曲线C的离心率.

Answer 1

解：（1）设.

       由题意得

       ∵m>1，∴轨迹C是中心在坐标原点，焦点在x轴上的椭圆（除去x轴上的两项点），其中长轴长为2，短轴长为2.

   （2）当m=时，曲线C的方程为

       由

       令

       此时直线l与曲线C有且只有一个公共点.

   （3）直线l方程为2x－y+3=0.

       设点表示P到点（1，0）的距离，d₂表示P到直线x=2的距离，

       则

      

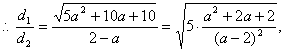
       令

       则

       令

      

       ∴的最小值等于椭圆的离心率。