题目内容
已知实数m>0,直线l: 与椭圆C:
与椭圆C: 相切于点P。
相切于点P。
(1)求实数m的值;
(2)若与l平行的直线l'与椭圆C交于点A,B,当a=2时,求 的最小值。
的最小值。
 与椭圆C:
与椭圆C: 相切于点P。
相切于点P。(1)求实数m的值;
(2)若与l平行的直线l'与椭圆C交于点A,B,当a=2时,求
 的最小值。
的最小值。解:(1)由题意可知方程组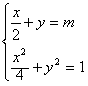
消去x得到的方程2y2-2my+m2-1=0有两个相等的实数根,
∴Δ=4m2-8(m2-1)=0,而m>0,故m=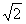 。
。
(2) 设直线l'的方程为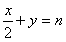
设A,B的坐标分别为(x1,y1),(x2,y2),
则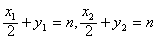 ,且y1,y2是方程组
,且y1,y2是方程组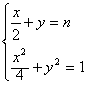
消去x 所得的方程2y2-2ay+n2-1=0的两个不同实根,
则Δ=4n2-8(n2-1)>0,
∴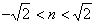 ,且
,且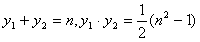
从而有x1+x2=2(n-y1)+2(n-y2)=2[2n-(y1+y2)]=2n,
x1·x2=2(n-y1)·2(n-y2)
=4[n2-n(y1+y2)+y1·y2]= 2(n2-1)
又由于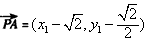 ,
,
∴令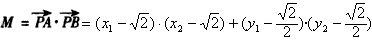
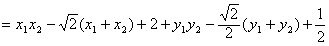
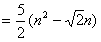
由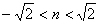 ,知M的最小值为
,知M的最小值为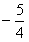
即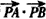 的最小值为
的最小值为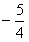 。
。
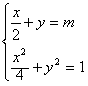
消去x得到的方程2y2-2my+m2-1=0有两个相等的实数根,
∴Δ=4m2-8(m2-1)=0,而m>0,故m=
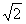 。
。(2) 设直线l'的方程为
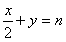
设A,B的坐标分别为(x1,y1),(x2,y2),
则
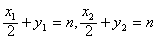 ,且y1,y2是方程组
,且y1,y2是方程组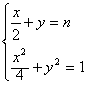
消去x 所得的方程2y2-2ay+n2-1=0的两个不同实根,
则Δ=4n2-8(n2-1)>0,
∴
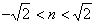 ,且
,且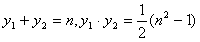
从而有x1+x2=2(n-y1)+2(n-y2)=2[2n-(y1+y2)]=2n,
x1·x2=2(n-y1)·2(n-y2)
=4[n2-n(y1+y2)+y1·y2]= 2(n2-1)
又由于
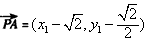 ,
,
∴令
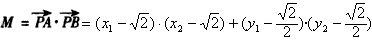
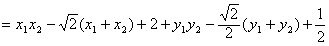
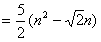
由
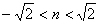 ,知M的最小值为
,知M的最小值为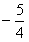
即
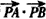 的最小值为
的最小值为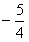 。
。
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 },若M
},若M R=Ф,则实数
R=Ф,则实数 的取值范围是( )
的取值范围是( )