题目内容
附加题:
(1)数列{an}的通项公式an=ncos
+1,前n项和为Sn,则S2012=
(2)已知x,y为正实数,且2x+8y-xy=0,则x+y的最小值为
(1)数列{an}的通项公式an=ncos
| nπ | 2 |
3018
3018
.(2)已知x,y为正实数,且2x+8y-xy=0,则x+y的最小值为
18
18
.分析:(1)先求出cos
的规律,进而得到ncos
的规律,即可求出数列的规律即可求出结论;
(2)将条件变形,与x+y相乘,展开利用均值不等式求解即可.
| nπ |
| 2 |
| nπ |
| 2 |
(2)将条件变形,与x+y相乘,展开利用均值不等式求解即可.
解答:解:(1)因为cos
=0,-1,0,1,0,-1,0,1…;
∴ncos
=0,-2,0,4,0,-6,0,8…;
∴ncos
的每四项和为2;
∴数列{an}的每四项和为:2+4=6.
而2012÷4=503;
∴S2012=503×6=3018;
(2)由2x+8y-xy=0,得2x+8y=xy,∴
+
=1,
∴x+y=(x+y)(
+
)=10≥10+2
=18,
当且仅当
=
,即x=2y时取等号,
又2x+8y-xy=0,∴x=12,y=6,
∴当x=12,y=6时,x+y取最小值18.
故答案为:(1)3018;(2)18
| nπ |
| 2 |
∴ncos
| nπ |
| 2 |
∴ncos
| nπ |
| 2 |
∴数列{an}的每四项和为:2+4=6.
而2012÷4=503;
∴S2012=503×6=3018;
(2)由2x+8y-xy=0,得2x+8y=xy,∴
| 2 |
| y |
| 8 |
| x |
∴x+y=(x+y)(
| 2 |
| y |
| 8 |
| x |
|
当且仅当
| 8y |
| x |
| 2x |
| y |
又2x+8y-xy=0,∴x=12,y=6,
∴当x=12,y=6时,x+y取最小值18.
故答案为:(1)3018;(2)18
点评:本题考查数列的求和,考查利用基本不等式求函数最值,解决本题的关键在于求出数列各项的规律.

练习册系列答案
相关题目
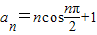 ,前n项和为Sn,则S2012= .
,前n项和为Sn,则S2012= .