题目内容
已知a,b,c是全不相等的正实数,求证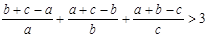

利用均值不等式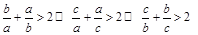 来分析证明即可。
来分析证明即可。
解析试题分析:解:∵ a,b,c全不相等
∴ 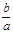 与
与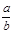 ,
,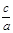 与
与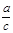 ,
,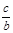 与
与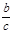 全不相等。
全不相等。
∴ 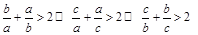
三式相加得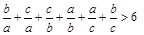
∴ 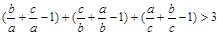
即 
考点:不等式的证明
点评:主要是考查了基本不等式的运用,来证明不等式,属于基础题。

练习册系列答案
相关题目
若不等式组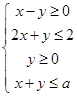 ,表示的平面区域是一个三角形区域,则
,表示的平面区域是一个三角形区域,则 的取值范围是( )
的取值范围是( )
A.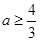 | B.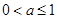 | C.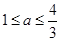 | D.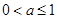 或 或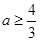 |
题目内容
已知a,b,c是全不相等的正实数,求证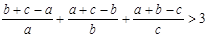

利用均值不等式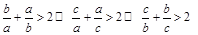 来分析证明即可。
来分析证明即可。
解析试题分析:解:∵ a,b,c全不相等
∴ 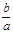 与
与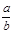 ,
,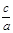 与
与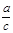 ,
,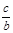 与
与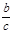 全不相等。
全不相等。
∴ 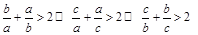
三式相加得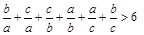
∴ 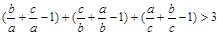
即 
考点:不等式的证明
点评:主要是考查了基本不等式的运用,来证明不等式,属于基础题。

若不等式组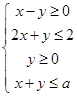 ,表示的平面区域是一个三角形区域,则
,表示的平面区域是一个三角形区域,则 的取值范围是( )
的取值范围是( )
A.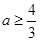 | B.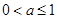 | C.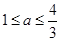 | D.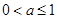 或 或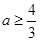 |