题目内容
设函数 是定义域为R的奇函数;
是定义域为R的奇函数;
(Ⅰ)若 ,试求不等式
,试求不等式 的解集;
的解集;
(Ⅱ)若 上的最小值为-2,
上的最小值为-2,
求m的值.
【答案】
 是定义域为R上的奇函数,
是定义域为R上的奇函数, …1分
…1分
(I) ,
,
 在R上为增函数
………………2分
在R上为增函数
………………2分
原不等式分为: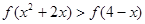

 …………5分
…………5分
(II) ,即
,即 (舍去)
(舍去)
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,由(1)可知f(x)=2x-2-x为增函数 ∵x≥1,∴t≥f(1)= ,
,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥ )
…………8分
)
…………8分
若m≥ ,当t=m时,h(t)min=2-m2=-2,∴m=2
,当t=m时,h(t)min=2-m2=-2,∴m=2
若m< ,当t=
,当t= 时,h(t)min=
时,h(t)min= -3m=-2,解得m=
-3m=-2,解得m=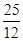 >
> ,舍去
,舍去
综上可知m=2.
【解析】略

练习册系列答案
相关题目
 是定义域为R的奇函数.
是定义域为R的奇函数. 的值;
的值; ,试判断函数单调性(不需证明)并求不等式
,试判断函数单调性(不需证明)并求不等式 的解集;
的解集; 上的最小值为
上的最小值为 ,求
,求 的值.
的值.  是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足 对一切
对一切 恒成立,当
恒成立,当 时,
时, .则下列四个命题中正确的命题是( )
.则下列四个命题中正确的命题是( )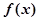 是以4为周期的周期函数;②
是以4为周期的周期函数;② 上的解析式为
上的解析式为 ;
; ;④
;④ 处的切线方程为
处的切线方程为 .
. 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足 对一切
对一切 恒成立,当
恒成立,当 时,
时, 。则下列四个命题中正确的命题是
。则下列四个命题中正确的命题是 是以4为周期的周期函数;②
是以4为周期的周期函数;②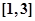 上的解析式为
上的解析式为 ;③
;③ ;④
;④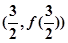 处的切线方程为
处的切线方程为 。
。 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足 对一切
对一切 恒成立,当
恒成立,当 时,
时, 。则下列四个命题中正确的命题是
。则下列四个命题中正确的命题是 是以4为周期的周期函数;②
是以4为周期的周期函数;② 上的解析式为
上的解析式为 ;③
;③ ;④
;④ 处的切线方程为
处的切线方程为 。
。