题目内容
(12分)已知过点 的动直线
的动直线 与圆
与圆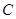 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
.
(1)求证:当 与
与 垂直时,
垂直时, 必过圆心
必过圆心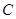 ;
;
(2)当 时,求直线
时,求直线 的方程;
的方程;
(3)探索 是否与直线
是否与直线 的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
【答案】
解:(1)∵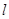 与
与 垂直,且
垂直,且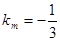 ,∴
,∴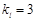 ,
,
故直线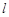 方程为
方程为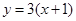 ,即
,即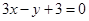 ………2分
………2分
∵圆心坐标(0,3)满足直线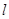 方程,
方程,
∴当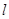 与
与 垂直时,
垂直时,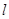 必过圆心
必过圆心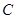 …………………
…4分
…………………
…4分
(2)①当直线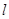 与
与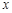 轴垂直时, 易知
轴垂直时, 易知 符合题意
符合题意
②当直线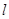 与
与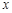 轴不垂直时,
轴不垂直时,
设直线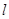 的方程为
的方程为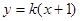 ,即
,即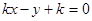 ,
,
∵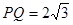 ,∴
,∴ ,
,
则由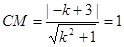 ,得
,得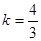 , ∴直线
, ∴直线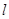 :
: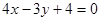 .
.
故直线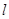 的方程为
的方程为 或
或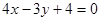 ………………………………………8分
………………………………………8分
(3)∵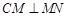 ,∴
,∴ 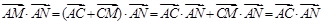
① 当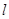 与
与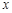 轴垂直时,易得
轴垂直时,易得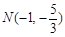 ,则
,则 ,又
,又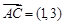 ,
,
∴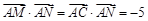
当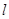 的斜率存在时,设直线
的斜率存在时,设直线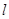 的方程为
的方程为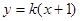 ,
,
则由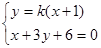 ,得
,得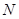 (
(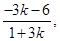
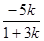 ),则
),则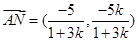
∴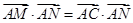 =
=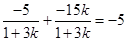
综上所述,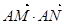 与直线
与直线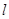 的斜率无关,且
的斜率无关,且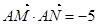 .…………………12分
.…………………12分
【解析】略

练习册系列答案
相关题目


 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
. 时,求直线
时,求直线 是否与直线
是否与直线 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
. 时,求直线
时,求直线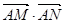 是否与直线
是否与直线