题目内容
已知过点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
:![]() 相交于
相交于![]() 、
、![]() 两点,
两点, ![]() 与
与
直线![]() :
:![]() 相交于
相交于![]() .
.
(1)求证:当![]() 与
与![]() 垂直时,
垂直时,![]() 必过圆心
必过圆心![]() ;
;
(2)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.

(2)直线![]() 的方程为
的方程为![]() 或
或![]()
解析:
(1)∵![]() 与
与![]() 垂直,且
垂直,且![]() ,∴
,∴![]() ,
,
故直线![]() 方程为
方程为![]() ,即
,即![]() ………3分
………3分
∵圆心坐标(0,3)满足直线![]() 方程,
方程,
∴当![]() 与
与![]() 垂直时,
垂直时,![]() 必过圆心
必过圆心![]() …………………5分
…………………5分
(2)①当直线![]() 与
与![]() 轴垂直时, 易知
轴垂直时, 易知![]() 符合题意………8分
符合题意………8分
②当直线![]() 与
与![]() 轴不垂直时, 设直线
轴不垂直时, 设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,……9分
,……9分
∵![]() ,∴
,∴![]() ,……………10分
,……………10分
则由![]() ,得
,得![]() , ∴直线
, ∴直线![]() :
:![]() .………13分
.………13分
故直线![]() 的方程为
的方程为![]() 或
或![]() …………………14分
…………………14分


练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
. 时,求直线
时,求直线 是否与直线
是否与直线 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
. 时,求直线
时,求直线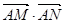 是否与直线
是否与直线
 的动直线
的动直线 与圆
与圆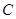 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
. 时,求直线
时,求直线 是否与直线
是否与直线