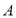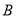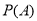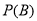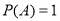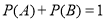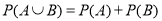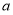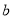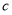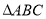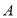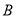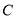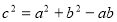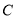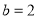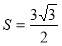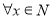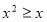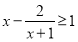题目内容
在平面直角坐标系中,已知点 ,点
,点 在直线
在直线 :
: 上运动,过点
上运动,过点 与
与 垂直的直线和线段
垂直的直线和线段 的垂直平分线相交于点
的垂直平分线相交于点 .
.
(1)求动点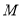 的轨迹
的轨迹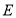 的方程;
的方程;
(2)过(1)中的轨迹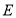 上的定点
上的定点
 作两条直线分别与轨迹
作两条直线分别与轨迹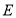 相交于
相交于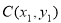 ,
, 两点.试探究:当直线
两点.试探究:当直线 ,
, 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线 的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
(1) 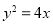 (2) 当直线
(2) 当直线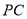 ,
,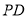 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线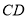 的斜率为定值
的斜率为定值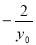
【解析】
试题分析:(1)由线段垂直平分线的性质知, 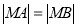 ,所以动点
,所以动点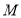 的轨迹
的轨迹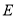 是以
是以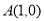 为焦点,直线
为焦点,直线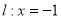 为准线的抛物线.易知其标准方程为
为准线的抛物线.易知其标准方程为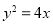 .
.
设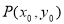 、
、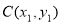 ,
,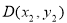 ,可由点差法求出
,可由点差法求出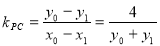 ,
,
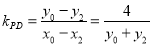 ,
,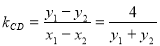
由直线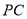 ,
,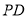 的倾斜角互补,得
的倾斜角互补,得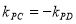
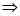
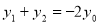
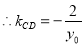 定值
定值
试题解析:(1)依题意,得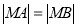 1分
1分
∴动点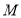 的轨迹
的轨迹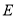 是以
是以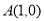 为焦点,直线
为焦点,直线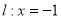 为准线的抛物线 3分
为准线的抛物线 3分
∴动点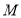 的轨迹
的轨迹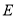 的方程为
的方程为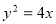 4分
4分
(2)∵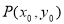 、
、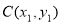 ,
,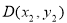 在抛物线
在抛物线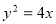 上
上
∴  5分
5分
由①-②得,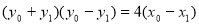
∴直线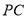 的斜率为
的斜率为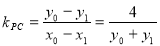 7分
7分
同理可得,直线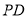 的斜率为
的斜率为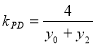 9分
9分
∴当直线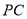 ,
,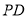 的倾斜角互补时,有
的倾斜角互补时,有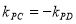
即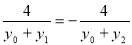
∴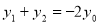 11分
11分
由②-③得,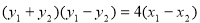
∴直线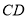 的斜率为
的斜率为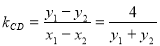 ④ 13分
④ 13分
将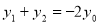 代入④,得
代入④,得 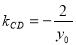
∴当直线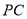 ,
,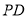 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线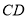 的斜率为定值
的斜率为定值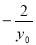 14分
14分
考点:1、抛物线的定义和标准方程;2、点差法的应用.

练习册系列答案
相关题目