题目内容
已知函数
(1)若 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)若定义在区间D上的函数 对于区间
对于区间 上的任意两个值
上的任意两个值 总有以下不等式
总有以下不等式 成立,则称函数
成立,则称函数 为区间
为区间 上的 “凹函数”.试证当
上的 “凹函数”.试证当 时,
时, 为“凹函数”.
为“凹函数”.
【答案】
(1)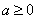 (2)理解凹函数的定义 ,然后结合中点函数值与任意两点的函数值和的关系式作差法加以证明。
(2)理解凹函数的定义 ,然后结合中点函数值与任意两点的函数值和的关系式作差法加以证明。
【解析】
试题分析:解(1)由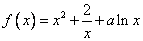 ,得
,得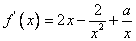
函数为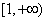 上单调函数. 若函数为
上单调函数. 若函数为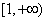 上单调增函数,则
上单调增函数,则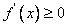 在
在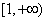 上恒成立,即不等式
上恒成立,即不等式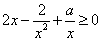 在
在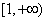 上恒成立. 也即
上恒成立. 也即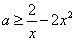 在
在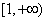 上恒成立.
上恒成立.
令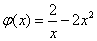 ,上述问题等价于
,上述问题等价于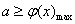 ,而
,而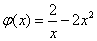 为在
为在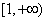 上的减函数,则
上的减函数,则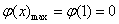 ,于是
,于是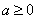 为所求.
为所求.
(2)证明:由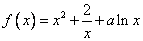 得
得
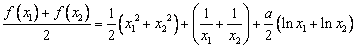
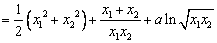
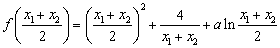
而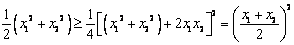 ①
①
又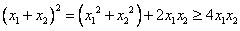 , ∴
, ∴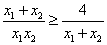 ②
②
∵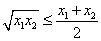 ∴
∴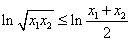 ,
,
∵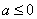 ∴
∴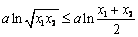 ③
③
由①、②、③得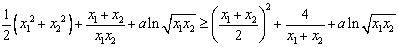
即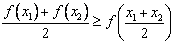 ,从而由凹函数的定义可知函数为凹函数
,从而由凹函数的定义可知函数为凹函数
考点:新定义和函数性质的运用
点评:结合均值不等式的思想,以及函数的解析式来求解,属于中档题。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
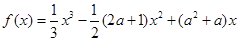 .
.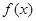 在
在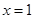 处取得极大值,求实数
处取得极大值,求实数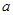 的值;
的值;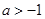 ,求
,求 上的最大值.
上的最大值. .
. 在
在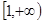 上是增函数,求实数
上是增函数,求实数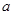 的取值范围;
的取值范围;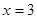 是
是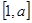 上的最小值和最大值.
上的最小值和最大值.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数