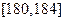题目内容
(本小题满分12分)
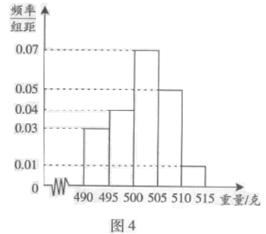
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六 组,第一组
组,第一组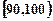 、第二组
、第二组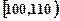 …第六组
…第六组 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组
中任意选2人,记他们的成绩分别
为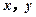 . 若
. 若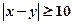 ,则称此二
,则称此二
人为“黄金帮扶组”,试求选出的二
人错误!链接无效。的概率 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于
120分的人数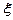 分布列及期望
分布列及期望 .
.
解:(Ⅰ)设第四,五组的频率分别为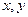 ,则
,则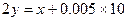 ①
① ②由①②解得
②由①②解得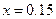 ,
,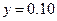 (2分)
(2分)
从而得出直方图(如图所示)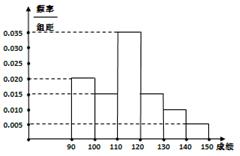 (3分)
(3分)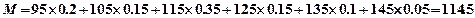 (4分)
(4分)
(Ⅱ)依题意第四组人数为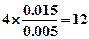 ,故
,故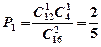 (6分)
(6分)
(Ⅲ)依题意样本总人数为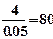 ,成绩不低于120分人数为
,成绩不低于120分人数为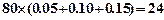 (7分)
(7分)
故在样本中任选1人,其成绩不低于120分的概率为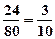 又由已知
又由已知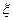 的可能取值为0,1,2,3
的可能取值为0,1,2,3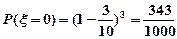 ,
,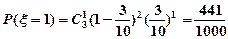 ,
,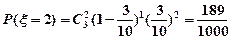 ,
,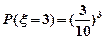 , 故
, 故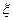 的分布列如下:
的分布列如下:
(10分)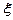
0 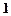
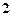
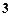
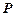
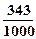
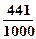
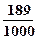
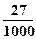
 依题意
依题意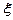 ~
~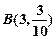 .故
.故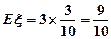 (12分)
(12分)
解析

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量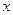 (吨)与相应的生产能耗
(吨)与相应的生产能耗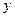 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
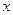 |  | 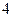 | 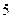 | 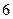 |
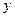 |  | 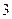 | 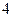 | 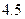 |
(2)请根据上表提供的数据,用最小二乘法求出
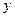 关于
关于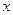 的线性回归方程
的线性回归方程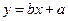 ;
;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
 (参考数值:
(参考数值: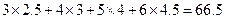 ,
,(
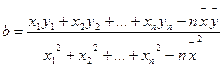 ,
,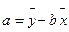 )
) (本题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班 位女同学,
位女同学, 位男同学中随机抽取一个容量为
位男同学中随机抽取一个容量为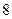 的样本进行分析。
的样本进行分析。
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(Ⅱ)随机抽取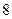 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: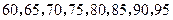 ;
;
物理成绩由低到高依次为: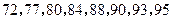 ,若规定
,若规定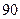 分(含
分(含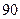 分)以
分)以 上为优秀,记
上为优秀,记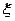 为这
为这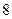 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求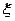 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若这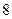 位同学的数学、物理分数事实上对应下表:
位同学的数学、物理分数事实上对应下表:
| 学生编号 |  | 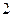 | 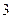 | 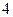 | 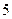 | 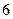 | 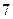 | 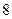 |
数学分数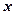 | 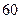 | 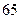 | 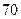 | 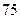 | 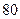 | 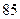 | 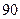 |  |
物理分数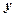 | 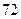 | 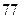 | 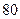 | 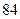 | 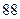 | 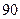 | 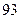 |  |
根据上表数据可知,变量
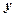 与
与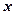
 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出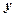 与
与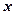 的线性回归方程(系数精确到
的线性回归方程(系数精确到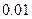 ).(参考公式:
).(参考公式: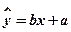 ,其中
,其中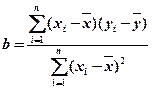 ,
,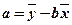 ; 参考数据:
; 参考数据: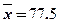 ,
,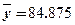 ,
,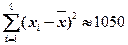 ,
, ,
,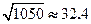 ,
,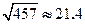 ,
,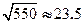 )
) (本题14分)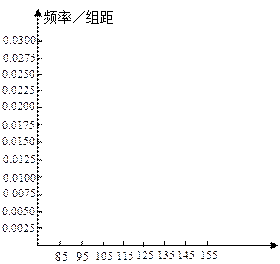 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
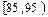 | ① | 0. 025 |
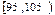 | | 0.050 |
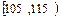 | | 0.200 |
 | 12 | 0.300 |
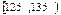 | | 0.275 |
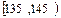 | 4 | ② |
| [145,155] | | 0.050 |
| 合计 | | ③ |
|
(1)根据上面图表,①②③处的数值分别为 ▲ 、 ▲ 、 ▲ ;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率.
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独 立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| | 爱看课外书 | 不爱看课外书 | 总计 |
作文水平 好 好 | | | |
| 作文水平一般 | [来源:学。科。网Z。X。X。K] | | |
| 总计 | | | |
 分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.参考公式:
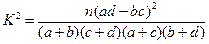 ,其中
,其中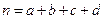 .
.参考数据:
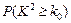 [来源:学*科*网] [来源:学*科*网] | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
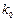 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 岁的人群随机抽取
岁的人群随机抽取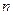 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: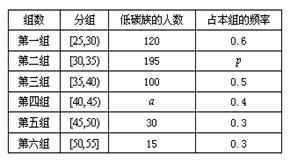
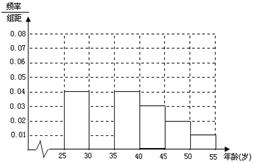
 、
、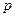 的值;
的值;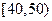 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取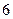 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取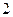 人作为领队,求选取的
人作为领队,求选取的 岁的概率。
岁的概率。