题目内容
(本题满分16分)第(1)小题满分6分,第(2)小题满分5分,第(3)小题满分5分。
已知函数![]() 。
。
(1)当![]() 时,画出函数
时,画出函数![]() 的大致图像,并写出其单调递增区间;
的大致图像,并写出其单调递增区间;
(2)若函数![]() 在
在![]() 上是单调递减函数,求实数
上是单调递减函数,求实数![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 |
解:(1)![]() 时,
时,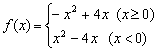 ,
,![]() 的图象如图,图象画出,-------------------3分
的图象如图,图象画出,-------------------3分
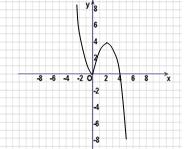 单调递增区间为
单调递增区间为![]() 。-------------------6分
。-------------------6分
(2)解一:设![]() ,
,
当![]() 在
在![]() 上单调递减时,
上单调递减时,![]() 对
对![]() 都成立,-------------------8分
都成立,-------------------8分
即![]() ,
,![]() 对
对![]() 都成立,-------------------10分
都成立,-------------------10分
所以![]() -------------------11分
-------------------11分
解二:数形结合方法:![]() 时,
时,![]() -------------------8分
-------------------8分
若函数![]() 在
在![]() 上是单调递减函数,则
上是单调递减函数,则![]() -------------------10分
-------------------10分
所以![]() -------------------11分
-------------------11分
(3)当![]() 时,
时,![]() 成立,所以
成立,所以![]() ; -------------------12分
; -------------------12分
当![]() 时,
时,![]() ,即
,即![]() ,只要
,只要![]() ; -------------------13分
; -------------------13分
设![]() ,
,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
当![]() 时,
时,![]() ;-------------------14分
;-------------------14分
所以![]() -------------------15分
-------------------15分
综上, ![]() 对
对![]() 恒成立的实数
恒成立的实数![]() 的取值范围是
的取值范围是![]() 。-------------------16分
。-------------------16分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,
,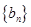 是等差数列,且
是等差数列,且 ,求非零常数
,求非零常数 ;
; ,求证:
,求证: .
.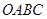 中,已知过点
中,已知过点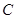 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若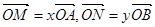 。
。 与
与 的关系为
的关系为 ;
; ,定义在
,定义在 上的偶函数
上的偶函数 ,当
,当 时
时 ,且函数
,且函数 对称,求证:
对称,求证: ,并求
,并求 时的解析式;
时的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。 、
、 为坐标平面
为坐标平面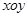 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点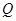 (异于
(异于 ,点
,点 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
; 在椭圆
在椭圆 上,试问:点
上,试问:点 、
、 是圆
是圆 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 是
是 轴正方向的单位向量,设
轴正方向的单位向量,设 =
= ,
,  =
= ,且满足
,且满足 .
. 的轨迹方程;
的轨迹方程; 的直线
的直线 交上述轨迹于
交上述轨迹于 两点,且
两点,且 ,求直线
,求直线