题目内容
某公司在开发的初级阶段大量生产一种产品.这种产品是否合格要进行A、B两项技术指标检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为| 5 |
| 12 |
| 11 |
| 12 |
(1)任意依次抽出5个产品进行检测,求其中至多3个产品是合格品的概率是多少;
(2)任意依次抽取该种产品4个,设ξ表示其中合格品的个数,求Eξ与Dξ.
分析:(1)设出两项指标达标的概率,根据有且仅有一项技术指标达标的概率为
,至少一项技术指标达标的概率为
,得到关于两个概率的关系式,解方程即可.再求出概率.
(2)由题意知每一次抽取一个产品相当于一次独立重复试验,变量符合二项分布,根据二项分布的期望和方差公式得到结果.
| 5 |
| 12 |
| 11 |
| 12 |
(2)由题意知每一次抽取一个产品相当于一次独立重复试验,变量符合二项分布,根据二项分布的期望和方差公式得到结果.
解答:解:(1)设A、B两项技术指标达标的概率分别为P1、P2
由题意得:
解得:P1=
,P2=
或P1=
,P2=
,
∴P=P1P2=
.
即,一个产品经过检测为合格品的概率为
任意抽出5个产品进行检查,其中至多3个产品是合格品的概率为1-
(
)5-
(
)5=
(2)依题意知ξ~B(4,
),Eξ=4×
=2,Dξ=4×
×
=1
由题意得:
|
解得:P1=
| 3 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
∴P=P1P2=
| 1 |
| 2 |
即,一个产品经过检测为合格品的概率为
| 1 |
| 2 |
任意抽出5个产品进行检查,其中至多3个产品是合格品的概率为1-
| C | 4 5 |
| 1 |
| 2 |
| C | 5 5 |
| 1 |
| 2 |
| 13 |
| 16 |
(2)依题意知ξ~B(4,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是看出变量符合二项分布,这样题目的计算过程就省去了,只要根据公式写出结果就可以.

练习册系列答案
相关题目
 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为 .按质量检验规定:两项技术指标都达标的产品为合格品.
.按质量检验规定:两项技术指标都达标的产品为合格品. ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为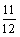 。按质量检验规定:两项技术指标都达标的产品为合格品。
。按质量检验规定:两项技术指标都达标的产品为合格品。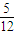 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为 .按质量检验规定:两项技术指标都达标的产品为合格品.
.按质量检验规定:两项技术指标都达标的产品为合格品.