题目内容
设α和β为不重合的两个平面,给出下列命题:
①若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
②若α外一条直线l与α内的一条直线平行,则l和α平行;
③设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
④直线l与α垂直的充分必要条件是l与α内的两条直线垂直.
上面命题中,真命题的序号是 (写出所有真命题的序号).
①若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
②若α外一条直线l与α内的一条直线平行,则l和α平行;
③设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
④直线l与α垂直的充分必要条件是l与α内的两条直线垂直.
上面命题中,真命题的序号是 (写出所有真命题的序号).
①②
命题①是两个平面平行的判定定理,正确;命题②是直线与平面平行的判定定理,正确;命题③中在α内可以作无数条直线与l垂直,但α与β只是相交关系,不一定垂直,错误;命题④中直线l与α垂直可推出l与α内两条直线垂直,但l与α内的两条直线垂直推不出直线l与α垂直,所以命题④不正确.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
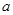 、
、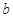 为不垂直的异面直线,
为不垂直的异面直线,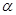 是一个平面,则
是一个平面,则
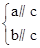 ⇒a∥b ②
⇒a∥b ② ⇒a∥b
⇒a∥b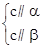 ⇒α∥β ④
⇒α∥β ④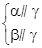 ⇒α∥β
⇒α∥β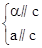 ⇒α∥a ⑥
⇒α∥a ⑥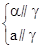 ⇒a∥α
⇒a∥α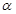 、
、 是不重合的平面,
是不重合的平面,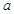 、
、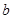 、
、 是不重合的直线,给出下列命题:
是不重合的直线,给出下列命题: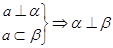 ;②
;② ;③
;③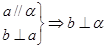 .
.