题目内容
当m为何实数时,复数Z=(2m+1)(m-2)+(m-1)(m-2)i是(1)实数;(2)虚数;(3)纯虚数;(4)对应点在x轴上方.
分析:(1)当这个复数是一个实数时,虚部等于0,解关于m的方程,得到结果.
(2)当这个复数是一个虚数时,实部等于0,解出关于m的方程,得到结果.
(3)当一个复数是一个纯虚数时,要使的实部等于0,且虚部不等于0,解出关于m的不等式组,得到结果.
(4)复数对应的点在横轴的上方,要使虚部大于0,解出关于m的一元二次不等式,得到结果.
(2)当这个复数是一个虚数时,实部等于0,解出关于m的方程,得到结果.
(3)当一个复数是一个纯虚数时,要使的实部等于0,且虚部不等于0,解出关于m的不等式组,得到结果.
(4)复数对应的点在横轴的上方,要使虚部大于0,解出关于m的一元二次不等式,得到结果.
解答:解:Z=(2m+1)(m-2)+(m-1)(m-2)i
(1)当m=1或m=2时,Z是实数.
(2)当m≠1且m≠2时,Z是虚数.
(3)当(m-1)(m-2)≠0,(2m+1)(m-2)=0,
即m=-
时,是一个纯虚数,
(4)对应点在x轴的上方,
有(m-1)(m-2)>0
∴m>2,m<1
(1)当m=1或m=2时,Z是实数.
(2)当m≠1且m≠2时,Z是虚数.
(3)当(m-1)(m-2)≠0,(2m+1)(m-2)=0,
即m=-
| 1 |
| 2 |
(4)对应点在x轴的上方,
有(m-1)(m-2)>0
∴m>2,m<1
点评:本题考查复数的基本概念,解题时要注意当一个复数是一个纯虚数时,要使的实部等于0且虚部不等于0,这一点容易漏掉.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
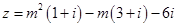 ,则当m为何实数时,复数z是
,则当m为何实数时,复数z是