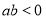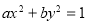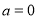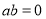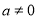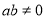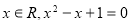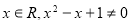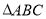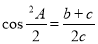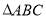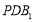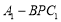题目内容
已知函数 ;
;
(1)若 >0,试判断f(x)在定义域内的单调性;
>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为 ,求
,求 的值;
的值;
(3)若f(x)<x2在(1, 上恒成立,求a的取值范围.
上恒成立,求a的取值范围.
(1)单调递增函数;(2) ;(3)
;(3)
【解析】
试题分析:(1)首先确定函数的定义域是 ,再求导数
,再求导数 =
=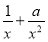 ,依题设中的条件判断
,依题设中的条件判断 的符号,从而得到
的符号,从而得到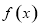 在定义域内的单调性;
在定义域内的单调性;
(2)由于 =
=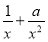 =
= ,根据参数
,根据参数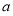 对导数的取值的影响,恰当地对其分类讨论,根据
对导数的取值的影响,恰当地对其分类讨论,根据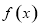 在
在 上的单调性,求出含参数
上的单调性,求出含参数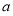 的最小值表达式,列方程求
的最小值表达式,列方程求 的值, 并注意检查其合理性;
的值, 并注意检查其合理性;
(3)由于
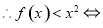
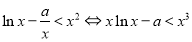
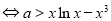
令 ,则可将原问题转化为求函数
,则可将原问题转化为求函数 的最大值问题,可借助导数进行探究.
的最大值问题,可借助导数进行探究.
试题解析:.【解析】
(1)由题意f(x)的定义域为(0,+∞),且f'(x)= …(2分)
…(2分)
∵a>0,
∴f'(x)>0,
故f(x)在(0,+∞)上是单调递增函数 …(4分)
(2)由(1)可知,f′(x)=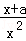 .
.
(1)若a≥﹣1,则x+a≥0,即f′(x)≥0在[1,e]上恒成立,此时f(x)在[1,e]上为增函数,
∴[f(x)]m1n=f(1)=﹣a=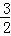 ,
,
∴a=﹣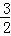 (舍去) …(5分)
(舍去) …(5分)
(2)若a≤﹣e,则x+a≤0,即f′(x)≤0在[1,e]上恒成立,此时f(x)在[1,e]上为减函数,
∴[f(x)]m1n=f(e)=1﹣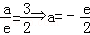 (舍去)…(6分)
(舍去)…(6分)
(3)若﹣e<a<﹣1,令f'(x)=0得x=﹣a,当1<x<﹣a时,f'(x)<0,
∴f(x)在(1,﹣a)上为减函数,f(x)在(﹣a,e)上为增函数,
∴[f(x)]m1n=f(﹣a)=ln(﹣a)+1=
∴[f(x)]m1n=f(﹣a)=ln(﹣a)+1=
∴a=﹣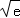 .…(8分)
.…(8分)
(3)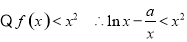
又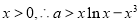 9分
9分
令
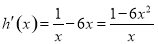
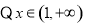 时,
时,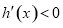
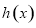 在
在 上是减函数 10分
上是减函数 10分

即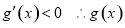 在
在 上也是减函数,
上也是减函数,
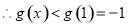
所以,当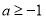 时,
时, 在
在 上恒成立
上恒成立
所以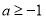 . 12分
. 12分
考点:1、导数在研究函数性质中的应用;2、等价转化的思想与分类讨论的思想.

 阅读快车系列答案
阅读快车系列答案