题目内容
如图,函数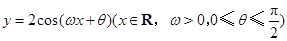 的图象与
的图象与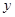 轴相交于点
轴相交于点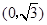 ,且该函数的最小正周期为
,且该函数的最小正周期为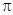 .
.

(1)、求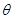 和
和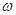 的值;
的值;
(2)、已知点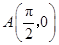 ,点
,点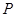 是该函数图象上一点,
是该函数图象上一点,
点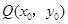 是
是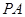 的中点,当
的中点,当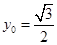 ,
,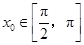 时,求
时,求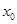 的值.
的值.
【答案】
(1) .
.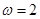 , (2)
, (2)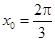 或
或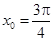 .
.
【解析】
试题分析:(1)将 ,
,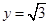 代入函数
代入函数
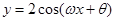 得
得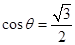 ,
,
因为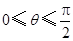 ,所以
,所以 .又因为该函数的最小正周期为
.又因为该函数的最小正周期为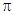 ,所以
,所以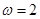 ,因此
,因此 .
.
(2)因为点 ,
,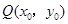 是
是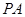 的中点,
的中点,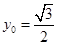 ,所以点
,所以点 的坐标为
的坐标为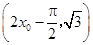 .又因为点
.又因为点 在
在 的图象上,所以
的图象上,所以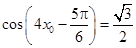 .因为
.因为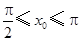 ,所以
,所以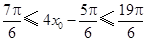 ,从而得
,从而得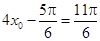 或
或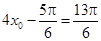 .即
.即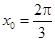 或
或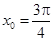 .
.
考点:三角函数图像与性质
点评:解决的关键是对于三角函数图像和解析式的关系的熟练的运用,同时能解三角方程,属于基础题。

练习册系列答案
相关题目

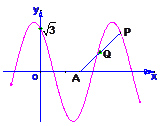 如图,函数
如图,函数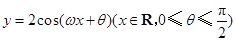 的图象与
的图象与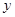 轴交于点
轴交于点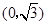 ,且最小正周期为π.
,且最小正周期为π.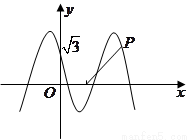
 和
和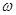 的值;(2)已知点
的值;(2)已知点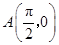 ,点
,点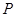 是该函数图象上一点,点
是该函数图象上一点,点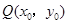 是
是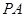 的中点,当
的中点,当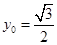 ,
,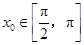 时,求
时,求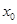 的值.
的值.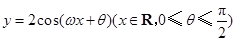 的图象与
的图象与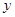 轴交于点
轴交于点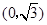 ,且最小正周期为π.
,且最小正周期为π.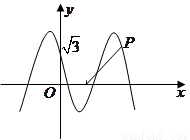
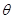 和
和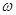 的值;(2)已知点
的值;(2)已知点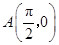 ,点
,点 是该函数图象上一点,点
是该函数图象上一点,点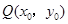 是
是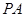 的中点,当
的中点,当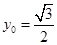 ,
,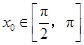 时,求
时,求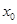 的值.
的值.