题目内容
6.已知椭圆x2+4y2=m上两点间的最大距离是8.则实数m的值为16.分析 椭圆x2+4y2=m化为$\frac{{x}^{2}}{m}+\frac{{y}^{2}}{\frac{m}{4}}=1$,由于$m>\frac{m}{4}$>0,可得a2=m.根据椭圆x2+4y2=m上两点间的最大距离是8.可得2a=8,解得即可.
解答 解:椭圆x2+4y2=m化为$\frac{{x}^{2}}{m}+\frac{{y}^{2}}{\frac{m}{4}}=1$,
∵$m>\frac{m}{4}$>0,
∴a2=m,因此a=$\sqrt{m}$.
∵椭圆x2+4y2=m上两点间的最大距离是8.
∴2a=2$\sqrt{m}$=8,解得m=16.
故答案为:16.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.5005×50065006-5006×50055005的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
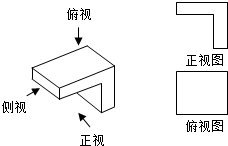 在如图中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确的吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求)
在如图中,图(b)是图(a)中实物画出的正视图和俯视图,你认为正确的吗?如果不正确,请找出错误并改正,然后画出侧视图(尺寸不作严格要求)