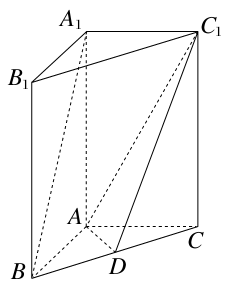
题目内容
如图1,直角梯形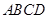 中,
中, ,
,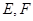 分别为边
分别为边 和
和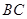 上的点,且
上的点,且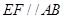 ,
,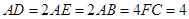 .将四边形
.将四边形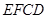 沿
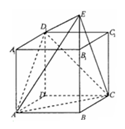
沿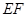 折起成如图2的位置,使
折起成如图2的位置,使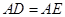 .
.
(1)求证: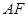
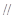 平面
平面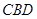 ;
;
(2)求平面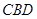 与平面
与平面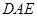 所成锐角的余弦值.
所成锐角的余弦值.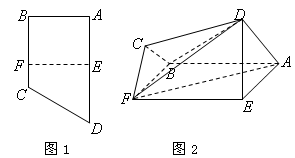
(1)见解析;(2)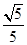 。
。
解析试题分析:(1)取DE中点G,连接FG,AG, 平面
平面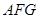 ,只需证平面AFG∥平面CBD,又
,只需证平面AFG∥平面CBD,又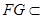 平面
平面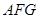 ,
,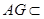 平面
平面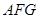 ,故只需证
,故只需证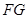 ∥平面CBD,
∥平面CBD, ∥平面CBD即可;
∥平面CBD即可;
(2)要求平面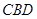 与平面
与平面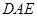 所成锐角的余弦值,需找两平面的法向量,取
所成锐角的余弦值,需找两平面的法向量,取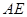 中点为H,连接DH,可证
中点为H,连接DH,可证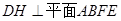 , 故以
, 故以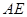 中点H为原点,
中点H为原点,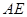 为
为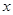 轴建立如图所示的空间直角坐标系,易知
轴建立如图所示的空间直角坐标系,易知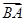 是平面
是平面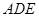 的一个法向量,由
的一个法向量,由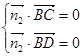 可得平面
可得平面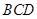 的一个法向量为
的一个法向量为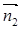 ,然后由空间两向量夹角公式去求平面
,然后由空间两向量夹角公式去求平面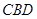 与平面
与平面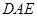 所成锐角的余弦值。
所成锐角的余弦值。
试题解析:(1)证明:取DE中点G,连接FG,AG,CG.因为 CF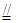 DG,所以FG∥CD.因为 CG
DG,所以FG∥CD.因为 CG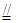 AB, ,
AB, ,
所以AG∥BC.所以平面AFG∥平面CBD, 所以 AF∥平面CBD.
(2)解: 取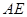 中点为H,连接DH.
中点为H,连接DH.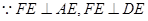 ,
,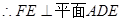 ,
,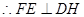 .
.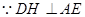 ,
,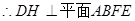 .
.
以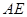 中点H为原点,
中点H为原点,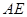 为
为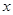 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则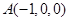 ,
,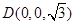 ,
,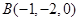 ,
,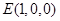 所以
所以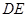 的中点坐标为
的中点坐标为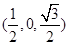 因为
因为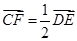 ,所以
,所以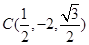 易知
易知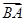 是平面
是平面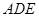 的一个法向量,
的一个法向量,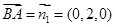 设平面
设平面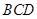 的一个法向量为
的一个法向量为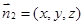
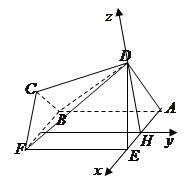
由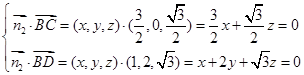
令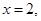 则
则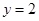 ,
,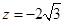 ,
,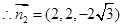
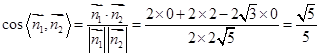 ,
,
所以面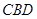 与面
与面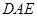 所成角的余弦值为
所成角的余弦值为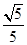 .
.
考点:(1)空间线面平行、面面平行、线面垂直判定定理的应用;(2)空间两平面夹角的定义、平面法向量的定义的应用;(3)空间向量的基本运算。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
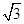 ,E是PB上任意一点.
,E是PB上任意一点.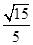 ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.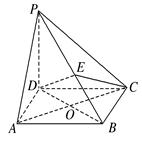
 中,
中, 分别是棱
分别是棱 的中点,点
的中点,点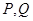 分别在棱
分别在棱 ,
,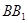 上移动,且
上移动,且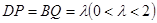 .
. 时,证明:直线
时,证明:直线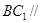 平面
平面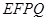 ;
; ,使平面
,使平面 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出
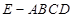 中,平面
中,平面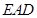
 平面
平面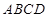 ,
,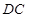 //
//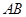 ,
,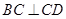 ,
,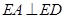 ,且
,且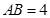 ,
,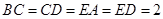 .
.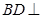 平面
平面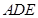 ;
;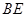 和平面
和平面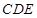 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点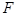 使得平面
使得平面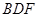
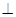 平面
平面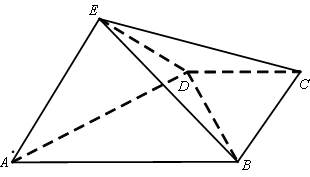
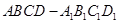 中,底面ABCD是边长为1的正方形,E为
中,底面ABCD是边长为1的正方形,E为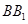 延长线上的一点且满足
延长线上的一点且满足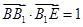 .
.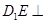 平面
平面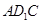 ;
;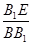 为何值时,二面角
为何值时,二面角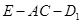 的大小为
的大小为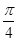 .
.
 AB.Q是PC上的一点,且PA∥平面QBD.
AB.Q是PC上的一点,且PA∥平面QBD.
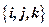 为单位正交基,且
为单位正交基,且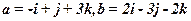 ,则向量
,则向量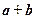 的坐标是______________________.
的坐标是______________________.