题目内容
 已知过抛物线x2=4y的焦点,斜率为k(k>0)的直线l交抛物线于A(x1,y2),B(x2,y2)(x1<x2)两点,且|AB|=8.
已知过抛物线x2=4y的焦点,斜率为k(k>0)的直线l交抛物线于A(x1,y2),B(x2,y2)(x1<x2)两点,且|AB|=8.(1)求直线l的方程;
(2)若点C(x3,y3)是抛物线弧AB上的一点,求△ABC面积的最大值,并求出点C的坐标.
分析:(1)由抛物线的方程即可得出焦点坐标,可设直线AB的方程y=kx+1,与抛物线方程联立得到根与系数的关系、利用抛物线的定义可得弦长公式,即可得出k.
(2)设与直线l平行的直线方程为y=x+m,由题意可知当该直线与抛物线相切时,该切点到直线l的距离最大,利用导数即可得出切点坐标,进而得到三角形的面积.
(2)设与直线l平行的直线方程为y=x+m,由题意可知当该直线与抛物线相切时,该切点到直线l的距离最大,利用导数即可得出切点坐标,进而得到三角形的面积.
解答: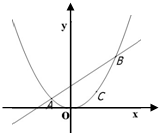 解:(1)抛物线x2=4y的焦点(0,1),
解:(1)抛物线x2=4y的焦点(0,1),
设直线AB的方程是y=kx+1,
联立
,整理得x2-4kx-4=0,
∴x1+x2=4k,
由抛物线定义得:|AB|=y1+y2+2=k(x1+x2)+4=8,
∴k2=1,k=±1.
∵k>0,∴k=1,直线方程为:y=x+1.
(2)设与直线l平行的直线方程为y=x+m,
由题意可知当该直线与抛物线相切时,该切点到直线l的距离最大,
y′=
x,令
x=1,解得x=2.
∴点C(2,1),点C到直线AB距离d=
,
(S△ABC)max=
•
•8=4
.
 解:(1)抛物线x2=4y的焦点(0,1),
解:(1)抛物线x2=4y的焦点(0,1),设直线AB的方程是y=kx+1,
联立
|
∴x1+x2=4k,
由抛物线定义得:|AB|=y1+y2+2=k(x1+x2)+4=8,
∴k2=1,k=±1.
∵k>0,∴k=1,直线方程为:y=x+1.
(2)设与直线l平行的直线方程为y=x+m,
由题意可知当该直线与抛物线相切时,该切点到直线l的距离最大,
y′=
| 1 |
| 2 |
| 1 |
| 2 |
∴点C(2,1),点C到直线AB距离d=
| 2 |
(S△ABC)max=
| 1 |
| 2 |
| 2 |
| 2 |
点评:熟练掌握抛物线的定义、标准方程及其性质、直线与抛物线的位置关系转化为方程联立得到根与系数的关系、弦长公式等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
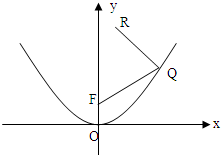 如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.
如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.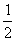 时,
时,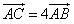 ,
,