题目内容
 已知棱长为1的正方体ABCD-A1B1C1D1,O为底ABCD对角线的交点.
已知棱长为1的正方体ABCD-A1B1C1D1,O为底ABCD对角线的交点.(Ⅰ)求证:A1C⊥平面AB1D1;
(Ⅱ)求A1到平面AB1D1的距离.
分析:(I)利用三垂线定理证明A1C垂直于平面AB1D1的两条相交直线,由线线垂直证明线面垂直;
(II)利用三棱锥的换底性,VA-A1B1D1=VA1-AB1D1,求三棱锥A1-AB1D1的高.
(II)利用三棱锥的换底性,VA-A1B1D1=VA1-AB1D1,求三棱锥A1-AB1D1的高.
解答: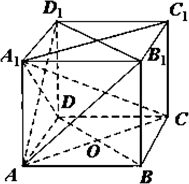 解:(I)证明:∵几何体ABCD-A1B1C1D1是正方体,∴CD⊥平面ADD1A1,
解:(I)证明:∵几何体ABCD-A1B1C1D1是正方体,∴CD⊥平面ADD1A1,
∴A1D为A1C在平面ADD1A1内的射影,∵A1D⊥AD1,
由三垂线定理得A1C⊥AD1,
同理可证A1C⊥B1D1,又B1D1∩AD1=D1,
∴A1C⊥平面AB1D1.
(II)∵棱长为1的正方体ABCD-A1B1C1D1,
∴△AB1D1为边长为
的等边三角形,
设A1到平面AB1D1的距离h,由三棱锥的换底性,
知VA-A1B1D1=VA1-AB1D1,即
×
×1×1×1=
×
×
×
×
×h,
解得h=
.
即A1到平面AB1D1的距离为
.
 解:(I)证明:∵几何体ABCD-A1B1C1D1是正方体,∴CD⊥平面ADD1A1,
解:(I)证明:∵几何体ABCD-A1B1C1D1是正方体,∴CD⊥平面ADD1A1,∴A1D为A1C在平面ADD1A1内的射影,∵A1D⊥AD1,
由三垂线定理得A1C⊥AD1,
同理可证A1C⊥B1D1,又B1D1∩AD1=D1,
∴A1C⊥平面AB1D1.
(II)∵棱长为1的正方体ABCD-A1B1C1D1,
∴△AB1D1为边长为
| 2 |
设A1到平面AB1D1的距离h,由三棱锥的换底性,
知VA-A1B1D1=VA1-AB1D1,即
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
解得h=
| ||
| 3 |
即A1到平面AB1D1的距离为
| ||
| 3 |
点评:本题考查了线面垂直的判定,考查了用三垂线定理证明线线垂直及用三棱锥的换底性求点到平面的距离,考查了学生的空间想象能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知棱长为1的正方体ABCD-A1B1C1D1.
如图,已知棱长为1的正方体ABCD-A1B1C1D1.