题目内容
若复数z与其共轭复数
满足:|z|=
,z+
=2则( )
. |
| z |
| 10 |
. |
| z |
| A、z2-2z+10=0 |
| B、z2+2z+10=0 |
| C、2z2+2z-10=0 |
| D、2z2-2z-10=0 |
分析:本题考查的知识点是复数的基本概率,由|z|=
,z+
=2,我们可以设Z=a+bi,则
=a-bi,然后根据已知条件,构造关于a,b的二元一次方程组,解方程组即可得到满足条件的复数Z的值,逐一代入四个答案,即可求出满足条件答案.
| 10 |
. |
| z |
. |
| Z |
解答:解:设Z=a+bi,则
=a-bi,
∵|z|=
,即a2+b2=10
z+
=2,即(a+bi)+(a-bi)=2a=2,
解得:a=1,b=±3
则Z=1+3i或Z=1-3i
则:z2-2z+10=0,故A正确
故选A
. |
| Z |
∵|z|=
| 10 |
z+
. |
| z |
解得:a=1,b=±3
则Z=1+3i或Z=1-3i
则:z2-2z+10=0,故A正确
故选A
点评:对于未知复数问题,我们可以先设Z=a+bi,则
=a-bi,我们可以根据已知条件结合复数相等的充要条件构造方程,解方程即可求出未知的向量.
. |
| Z |

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
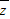 满足:
满足: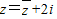 ,则复数z的虚部为( )
,则复数z的虚部为( ) 满足::
满足:: ,
, ,则( )
,则( )