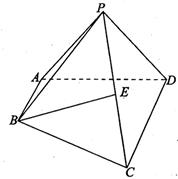
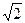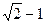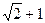题目内容
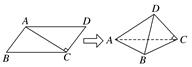
已知四棱锥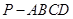 中,底面
中,底面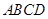 为直角梯形,
为直角梯形,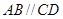 .
.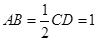 ,
,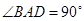 ,
,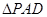 为正三角形,且面
为正三角形,且面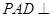 面
面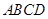 ,异面直线
,异面直线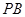 与
与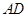 所成的角的余弦值为
所成的角的余弦值为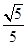 ,
,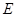 为
为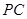 的中点.
的中点.
(Ⅰ)求证: 面
面 ;
;
(Ⅱ)求点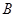 到平面
到平面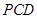 的距离;
的距离;
(Ⅲ)求平面 与平面
与平面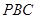 相交所成的锐二面角的大小.
相交所成的锐二面角的大小.
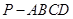 中,底面
中,底面 为直角梯形,
为直角梯形, .
.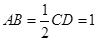 ,
,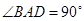 ,
,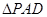 为正三角形,且面
为正三角形,且面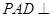 面
面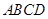 ,异面直线
,异面直线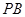 与
与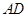 所成的角的余弦值为
所成的角的余弦值为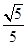 ,
,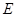 为
为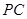 的中点.
的中点.(Ⅰ)求证:
 面
面 ;
;(Ⅱ)求点
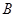 到平面
到平面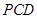 的距离;
的距离;(Ⅲ)求平面
 与平面
与平面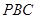 相交所成的锐二面角的大小.
相交所成的锐二面角的大小.
(1)取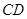 中点为
中点为 ,由于
,由于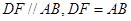 ,所以
,所以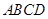 为平行四边形
为平行四边形
所以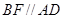 ,又因为
,又因为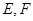 分别是
分别是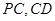 的中点,所以
的中点,所以 。所以面
。所以面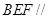 面
面 ,所以
,所以 面
面
(2)因为 ,
,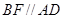 所以
所以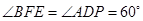 ,在
,在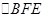 中,
中,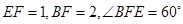 ,可得
,可得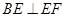 ,又因为面
,又因为面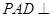 面
面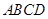 ,且
,且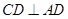 所以
所以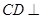 面
面 ,所以
,所以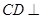 面
面 ,所以
,所以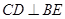 ,所以
,所以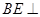 面
面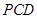 ,所以
,所以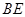 即为点
即为点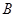 到面
到面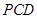 的距离,在
的距离,在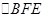 中可解得,
中可解得,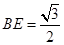
(3)设面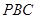 与面
与面 所成二面角为
所成二面角为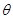 ,因为
,因为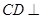 面
面 ,
,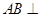 面
面 则面
则面 是面
是面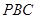 的射影,则
的射影,则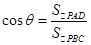 =
=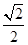 ,所以面
,所以面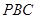 与面
与面 所成二面角为
所成二面角为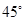
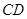 中点为
中点为 ,由于
,由于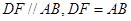 ,所以
,所以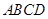 为平行四边形
为平行四边形所以
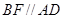 ,又因为
,又因为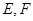 分别是
分别是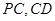 的中点,所以
的中点,所以 。所以面
。所以面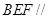 面
面 ,所以
,所以 面
面
(2)因为
 ,
,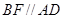 所以
所以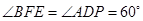 ,在
,在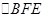 中,
中,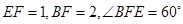 ,可得
,可得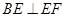 ,又因为面
,又因为面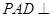 面
面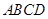 ,且
,且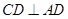 所以
所以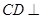 面
面 ,所以
,所以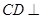 面
面 ,所以
,所以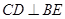 ,所以
,所以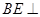 面
面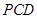 ,所以
,所以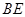 即为点
即为点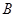 到面
到面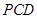 的距离,在
的距离,在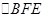 中可解得,
中可解得,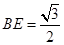
(3)设面
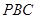 与面
与面 所成二面角为
所成二面角为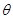 ,因为
,因为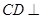 面
面 ,
,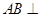 面
面 则面
则面 是面
是面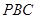 的射影,则
的射影,则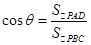 =
=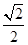 ,所以面
,所以面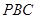 与面
与面 所成二面角为
所成二面角为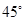
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

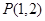 的直线
的直线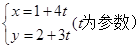 ,与圆
,与圆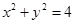 相较于A、B两点,则
相较于A、B两点,则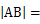 ________________。
________________。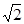 ,BB1=2,
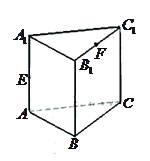
,BB1=2,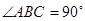 ,
,
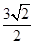
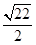
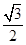
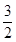
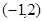 到直线
到直线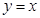 的距离是( )
的距离是( )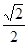
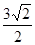
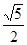
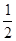
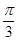 ,则A1C的长
,则A1C的长 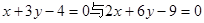 的距离是
的距离是 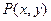 满足:
满足: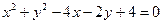 ,则点P到直线
,则点P到直线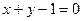 的最短距离是( )
的最短距离是( )