题目内容
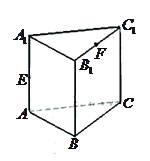
如图,在直三棱柱ABC—A1B1C1中,AB=BC=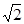 ,BB1=2,
,BB1=2,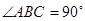 ,
,
E,F分别为AA1,C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为( )
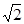 ,BB1=2,
,BB1=2,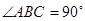 ,
,E,F分别为AA1,C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为( )

A.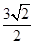 | B.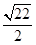 | C.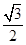 | D.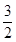 |
A
解:直三棱柱底面为等腰直角三角形,若把面ABA1B1和面B1C1BC展开在同一个平面内,
线段EF就在直角三角形A1EF中,由勾股定理得 EF2= A1E2+A1F2 = 【1+(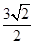 )2】2 = (
)2】2 = (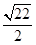 )2
)2
若把把面ABA1B1和面A1B1C展开在同一个平面内,设BB1的中点为G,则线段EF就在直角三角形EFG中,
由勾股定理得 EF=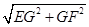 =
=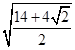
若把把面ACC1A1和面A1B1C1展开在同一个面内,过F作与CC1行的直线,过E作与AC平行的直线,所作的两线交与
点H,则EF就在直角三角形EFH中,由勾股定理得 EF= =
= 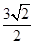
综上,从E到F两点的最短路径的长度为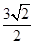 ,故答案为:
,故答案为: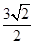
线段EF就在直角三角形A1EF中,由勾股定理得 EF2= A1E2+A1F2 = 【1+(
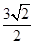 )2】2 = (
)2】2 = (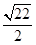 )2
)2若把把面ABA1B1和面A1B1C展开在同一个平面内,设BB1的中点为G,则线段EF就在直角三角形EFG中,
由勾股定理得 EF=
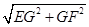 =
=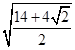
若把把面ACC1A1和面A1B1C1展开在同一个面内,过F作与CC1行的直线,过E作与AC平行的直线,所作的两线交与
点H,则EF就在直角三角形EFH中,由勾股定理得 EF=
 =
= 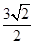
综上,从E到F两点的最短路径的长度为
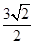 ,故答案为:
,故答案为: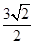

练习册系列答案
相关题目
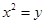 上的点到直线
上的点到直线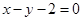 的最短距离为________________。
的最短距离为________________。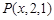 到
到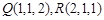 的距离相等,则
的距离相等,则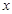 的值为 .
的值为 .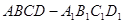 的三条棱
的三条棱 所在直线的距离相等的点
所在直线的距离相等的点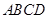 中,点
中,点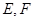 分别在线段
分别在线段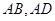 上,
上,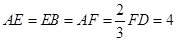 .沿直线
.沿直线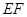 将
将 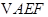 翻折成
翻折成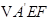 ,使平面
,使平面 .
.
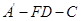 的余弦值;
的余弦值;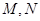 分别在线段
分别在线段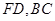 上,若沿直线
上,若沿直线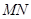 将四边形
将四边形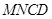 向上翻折,使
向上翻折,使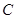 与
与 重合,求线段
重合,求线段 的长。
的长。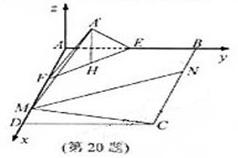
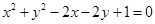 上的点到直线
上的点到直线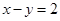 的距离最大值是
的距离最大值是 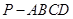 中,底面
中,底面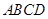 为直角梯形,
为直角梯形,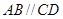 .
.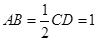 ,
,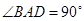 ,
,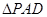 为正三角形,且面
为正三角形,且面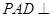 面
面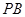 与
与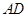 所成的角的余弦值为
所成的角的余弦值为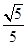 ,
,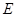 为
为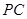 的中点.
的中点. 面
面 ;
;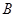 到平面
到平面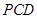 的距离;
的距离;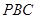 相交所成的锐二面角的大小.
相交所成的锐二面角的大小.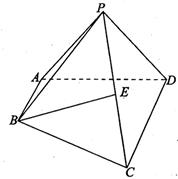
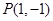 到直线3x-4y-5=0的距离是 .
到直线3x-4y-5=0的距离是 .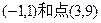 的距离是( )
的距离是( )