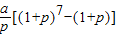题目内容
某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入a元定期储蓄,若年利率为P,且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年5月10日将所有存款和利息全部取回,则可取回的钱的总数(元)为( )
分析:先求出第一年存的钱到期可以取金额,第二年存的钱到期可以取金额,从而得到所求可取回的钱的金额,然后利用等比数列的求和公式解之即可.
解答:解:第一年存的钱到期可以取:a(1+p)7,
第二年存的钱到期可以取:a(1+p)6,
…
可取回的钱的总数:
a(1+p)7+a(1+p)6+…+a(1+p)
=
=
[(1+p)8-(1+p)].
故选D.
第二年存的钱到期可以取:a(1+p)6,
…
可取回的钱的总数:
a(1+p)7+a(1+p)6+…+a(1+p)
=
| a(1+p)[1-(1+p)7] |
| 1-(1+p) |
=
| a |
| p |
故选D.
点评:本题主要考查了等比数列的性质和应用,以及等比数列的求和,同时考查了计算能力,解题时要认真审题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B.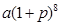 C.
C. D.
D.