题目内容
定义域为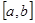 的函数
的函数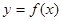 图象上两点
图象上两点 是
是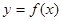 图象上任意一点,其中
图象上任意一点,其中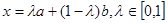 .已知向量
.已知向量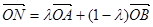 ,若不等式
,若不等式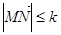 对任意
对任意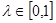 恒成立,则称函数
恒成立,则称函数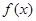 在
在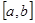 上“k阶线性近似”.若函数
上“k阶线性近似”.若函数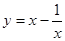 在
在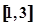 上“k阶线性近似”,则实数的k取值范围为( )
上“k阶线性近似”,则实数的k取值范围为( )
A.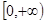 | B.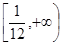 | C.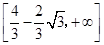 | D.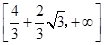 |
C
解析试题分析:由题意可得点N与在直线AB上,并且由点M的横坐标为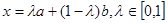 .又向量
.又向量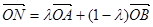 ,可得点N的横坐标也为
,可得点N的横坐标也为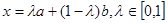 所以点M,N在横坐标相同.所以符合不等式
所以点M,N在横坐标相同.所以符合不等式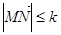 对任意
对任意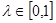 恒成立,则称函数
恒成立,则称函数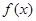 在
在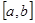 上的
上的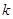 既要大于或等于
既要大于或等于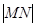 的最大值,这是解题的关键.由函数
的最大值,这是解题的关键.由函数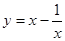 在
在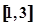 则
则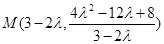 ,
,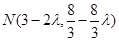
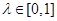 .所以
.所以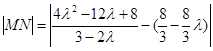 =
=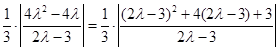 =
=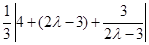 .又因为
.又因为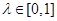 .所以
.所以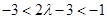 即求
即求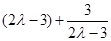 .…
.… 的最大值由打钩函数可得
的最大值由打钩函数可得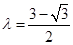 时
时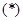 式的最大值是
式的最大值是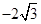 .所以
.所以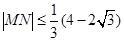 .所以
.所以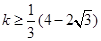 .故选C.
.故选C.
考点:1.向量的知识.2.新定义问题.3.函数的最值.4.恒成立问题.5.大钩函数求最值.

练习册系列答案
相关题目
若函数 为偶函数,且函数
为偶函数,且函数 在
在 上单调递增,则实数
上单调递增,则实数 的值为( )
的值为( )
A. | B. | C. | D. |
已知 ,
, ,
, ,则( )
,则( )
A. | B. |
C. | D. |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A.( ) ) | B.( ) ) | C.( ) ) | D.( ) ) |
下列函数中,既是偶函数又在区间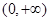 上单调递减的是__________.
上单调递减的是__________.
A.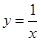 | B.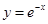 | C.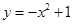 | D.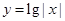 |
已知函数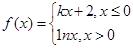 ,若
,若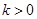 ,则函数
,则函数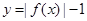 的零点个数是( )
的零点个数是( )
| A.1 | B.2 | C.3 | D.4 |
.定义在 上的偶函数
上的偶函数 ,当
,当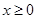 x≥0时,
x≥0时, ,则满足
,则满足 的x取值范围是( )
的x取值范围是( )
| A.(-1,2) | B.(-2,1) | C.[-1,2] | D.(-2,1] |
下列函数中,在定义域上既是奇函数又是增函数的为( )
A. | B. | C. | D. |
 ,
,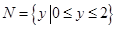 ,给出下列四个图形,其中能表示以
,给出下列四个图形,其中能表示以 为定义域,
为定义域, 为值域的函数关系的是( ).
为值域的函数关系的是( ).