题目内容
【题目】已知椭圆![]()
![]()
![]() 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2) 设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:可以巧用离心率,不妨设![]() ,由短轴的一个端点到右焦点的距离为
,由短轴的一个端点到右焦点的距离为![]()
![]() ,
,![]() ,则
,则![]() ,所以椭圆C的方程为
,所以椭圆C的方程为![]() ,第二步先设直线
,第二步先设直线![]() 的方程为
的方程为![]() ,联立方程组消去
,联立方程组消去![]() 后得关于
后得关于![]() 的一元二次方程,写出
的一元二次方程,写出![]() ,写出弦长
,写出弦长![]() 的表达式,又坐标原点O到L的距离的
的表达式,又坐标原点O到L的距离的![]() ,得到一个
,得到一个![]() 和
和![]() 的等量关系,代入面积表达式后,借助均值不等式求出最大值即可.
的等量关系,代入面积表达式后,借助均值不等式求出最大值即可.
试题解析:解:(1)设椭圆的半焦距为![]() ,依题意
,依题意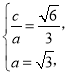
![]() ,
,
![]() 所求椭圆方程为
所求椭圆方程为![]() .
.
(2)设![]() ,
,![]() .
.
①当![]() 轴时,
轴时,![]() 为
为![]() ,代入
,代入![]() .
.
得![]()
![]() ,
, ![]()
②当![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() .
.
由已知![]() ,得
,得![]()
把![]() 代入椭圆方程,整理得
代入椭圆方程,整理得![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]()
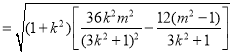
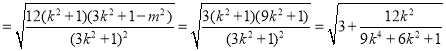
当![]() 时,
时,![]() ,
,
当![]() 时,
时, 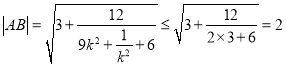
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
综上所述![]() .
.
![]() 当
当![]() 最大时,
最大时,![]() 面积取最大值
面积取最大值![]() .
.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响.部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
经计算![]() ,则下列选项正确的是( )
,则下列选项正确的是( )
A.有99.5%的把握认为使用智能手机对学习有影响
B.有99.5%的把握认为使用智能手机对学习无影响
C.有99.9%的把握认为使用智能手机对学习有影响
D.有99.9%的把握认为使用智能手机对学习无影响