题目内容
双曲线的虚轴长为4，离心率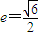
，F1、F2分别是它的左、右焦点，若过F1的直线与双曲线的左支交于A、B两点，且|AB|是|AF2|与|BF2|的等差中项，则|AB|等于（ ）A．
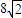
B．
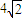
C．
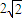
D．8
【答案】分析：由题意及双曲线的方程知双曲线的虚轴长为4，即2b=4，利用离心率的知求解出a的值，再利用|AB|是|AF2|与|BF2|的等差中项，得到|AB|．
解答：解：由题意可知
，于是
，
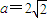∵2|AB|=|AF2|+|BF2|，
∴|AB|+|AF1|+|BF1|=|AF2|+|BF2|，
得|AB|=|AF2|-|AF1|+|BF2|-|BF1|=4a=8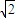
．
故选A．
点评：此题重点考查了双曲线方程的虚轴的概念及离心率的概念，还考查了利用双曲线的第一定义求解出|AB|的大小．
解答：解：由题意可知
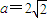，于是，∵2|AB|=|AF2|+|BF2|，
∴|AB|+|AF1|+|BF1|=|AF2|+|BF2|，
得|AB|=|AF2|-|AF1|+|BF2|-|BF1|=4a=8
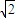．故选A．
点评：此题重点考查了双曲线方程的虚轴的概念及离心率的概念，还考查了利用双曲线的第一定义求解出|AB|的大小．
练习册系列答案
习题精选系列答案
相关题目
,F1、F2分别是它的左、右焦点，若过F1的直线与双曲线的左支交于A、B两点，且|AB|是|AF2|与|BF2|的等差中项，则|AB|等于（ ）
Ｂ.
Ｃ.
Ｄ.8
,
、
分别是它的左、右焦点,若过
是
与
的等差中项,则
C.
D. 
，
、
分别是它的左、右焦点，若过
是
的等差中项，则
B．
C．
D．8．
，F1、F2分别是它的左、右焦点，若过F1的直线与双曲线的左支交于A、B两点，且|AB|是|AF2|与|BF2|的等差中项，则|AB|等于（ ）
