题目内容
已知M(0,-2),点A在x轴上,点B在y轴的正半轴,点P在直线AB上,且满足 =
= ,
, =0.
=0.(1)当A点在x轴上移动时,求动点P的轨迹C的方程;
(2)过(-2,0)的直线l与轨迹C交于E、F两点,又过E、F作轨迹C的切线l1、l2,当l1⊥l2时,求直线l的方程.
【答案】分析:(1)设P(x,y),A(xA,0),B(0,yB),yB>0.则 =(x-xA,y),
=(x-xA,y), =(-x,yB-y).由
=(-x,yB-y).由 =
= ,得xA=2x,yB=2y.由
,得xA=2x,yB=2y.由 =0得到动点P的轨迹C的方程.
=0得到动点P的轨迹C的方程.
(2)设E(x1,y1),F(x2,y2),因为y′=2x,故两切线的斜率分别为2x1、2x2.由方程组 得x2-kx-2k=0,然后由根与系数的关系能够导出直线l的方程.
得x2-kx-2k=0,然后由根与系数的关系能够导出直线l的方程.
解答:解:(1)设P(x,y),A(xA,0),B(0,yB),yB>0.则 =(x-xA,y),
=(x-xA,y), =(-x,yB-y).
=(-x,yB-y).
由 =
= ,得
,得
即xA=2x,yB=2y.
又 =(xA,2),
=(xA,2), =(x-xA,y),
=(x-xA,y),
∴ =(2x,2),
=(2x,2), =(-x,y).
=(-x,y).
由 =0得x2=y(y≥0).
=0得x2=y(y≥0).
(2)设E(x1,y1),F(x2,y2),
因为y′=2x,故两切线的斜率分别为2x1、2x2.
由方程组
得x2-kx-2k=0,
x1+x2=k,x1x2=-2k.
当l1⊥l2时,4x1x2=-1,所以k= .
.
所以,直线l的方程是y= (x+2).
(x+2).
点评:本题考查圆锥曲线的性质和应用,解题时要注意挖掘隐含条件,根据实际情况注意公式的灵活运用.
 =(x-xA,y),
=(x-xA,y), =(-x,yB-y).由
=(-x,yB-y).由 =
= ,得xA=2x,yB=2y.由
,得xA=2x,yB=2y.由 =0得到动点P的轨迹C的方程.
=0得到动点P的轨迹C的方程.(2)设E(x1,y1),F(x2,y2),因为y′=2x,故两切线的斜率分别为2x1、2x2.由方程组
 得x2-kx-2k=0,然后由根与系数的关系能够导出直线l的方程.
得x2-kx-2k=0,然后由根与系数的关系能够导出直线l的方程.解答:解:(1)设P(x,y),A(xA,0),B(0,yB),yB>0.则
 =(x-xA,y),
=(x-xA,y), =(-x,yB-y).
=(-x,yB-y).由
 =
= ,得
,得
即xA=2x,yB=2y.
又
 =(xA,2),
=(xA,2), =(x-xA,y),
=(x-xA,y),∴
 =(2x,2),
=(2x,2), =(-x,y).
=(-x,y).由
 =0得x2=y(y≥0).
=0得x2=y(y≥0).(2)设E(x1,y1),F(x2,y2),
因为y′=2x,故两切线的斜率分别为2x1、2x2.
由方程组

得x2-kx-2k=0,
x1+x2=k,x1x2=-2k.
当l1⊥l2时,4x1x2=-1,所以k=
 .
.所以,直线l的方程是y=
 (x+2).
(x+2).点评:本题考查圆锥曲线的性质和应用,解题时要注意挖掘隐含条件,根据实际情况注意公式的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =
= ,
,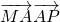 =0.
=0.