题目内容
在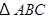 中,
中,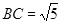
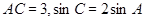 .
.
(1)求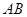 的值;
的值;
(2)求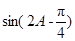 的值.
的值.
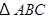 中,
中,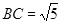
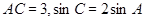 .
.(1)求
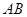 的值;
的值;(2)求
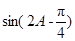 的值.
的值.(1)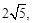 (2)
(2)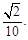
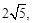 (2)
(2)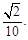
试题分析:(1)解三角形问题,通常利用正余弦定理进行边角转化.由正弦定理得:
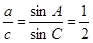 ,
,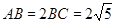 .(2)由(1)及条件知三角形三边,故用余弦定理求角. 由
.(2)由(1)及条件知三角形三边,故用余弦定理求角. 由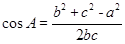 ,得
,得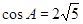 ,由同角三角函数关系,可得
,由同角三角函数关系,可得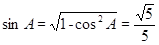 ,再由二倍角公式得到
,再由二倍角公式得到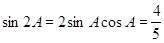 ,
,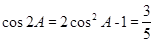 ,因此=
,因此=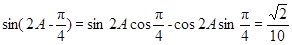 .
.试题解析:(1)因为
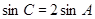 ,
,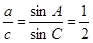
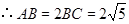
(2)
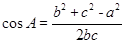 =
=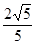
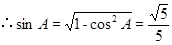
所以
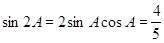 ,
, 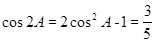

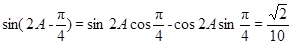

练习册系列答案
相关题目
 的终边经过点
的终边经过点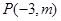 ,且
,且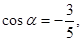
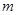 的值.(2)求
的值.(2)求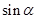 与
与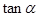 的值.
的值.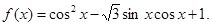
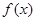 的单调递增区间;
的单调递增区间;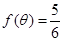 ,
,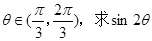 的值.
的值.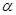 为锐角,且
为锐角,且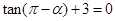 ,则
,则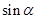 的值( )
的值( )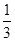
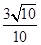
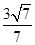
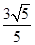
 ,且
,且 ≤θ≤
≤θ≤ ,则cos2θ=________.
,则cos2θ=________.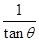 =4,则sin2θ=( )
=4,则sin2θ=( )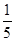
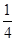
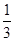
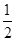
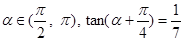 ,则
,则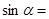 ( )
( )



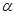 为第四象限的角,且
为第四象限的角,且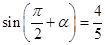 ,则
,则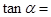 .
.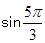 的值是( )
的值是( )