Question

（08年湖南六校联考文）已知方向向量为的直线l过点和椭圆

的焦点，且椭圆C的中心关于直线的对称点在椭圆C的右准线上．

    （1）求椭圆C的方程；

    （2）若A、B为椭圆的左、右顶点，为椭圆上异于A、B的动点，直线、分别交右准线于H、G，F为右焦点，求

    （3）是否存在过点的直线交椭圆C于，满足，若存在，求出的方程；若不存在，请说明理由．

Answer 1

解析：（1）直线

    原点关于的对称点为，在椭圆右准线上

    ，又焦点在上，焦点坐标为，即

    椭圆方程为     （3分）

    （2）设

     

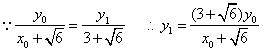
    同理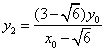

        

   

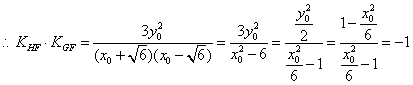
              （7分）

                                           

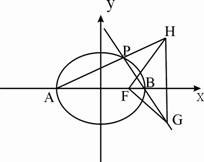
（3）设

    当直线斜率存在时，代入，

整理得

   

   

   

   

点O到直线的距离

   

    即

   

   

    即

   

    当直线垂直于轴时，，也满足

    经检验，上述三种情况对应的三条直线均满足，

故所求直线方程为

    或或         （14分）