题目内容
(本小题满分15分)已知函数 ,
,
(Ⅰ)判断函数
 的奇偶性;
的奇偶性;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若关于 的方
的方
 程
程 有实数解,求实数
有实数解,求实数 的取值范围.
的取值范围.
解:(Ⅰ)函数 的定义域为{
的定义域为{ 且
且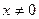 }
}  ∴
∴ 为偶函数
为偶函数
(Ⅱ)当 时,
时,
若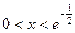 ,则
,则 ,
, 递减;
递减;
若 , 则
, 则 ,
, 递增.
递增.
再由 是偶函数,
是偶函数,
得 的递增区
的递增区 间是
间是 和
和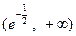 ;
;
递减区间是 和
和 .
.
(Ⅲ)由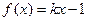 ,得:
,得: 令
令

当 ,
,
 显然
显然
 时,
时,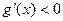 ,
,
 时,
时,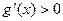 ,
,
∴ 时,
时, [来源:学。科。网]
[来源:学。科。网]
又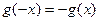 ,
,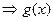 为奇函数 ∴
为奇函数 ∴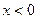 时,
时,
∴ 的值域为(-∞,-1]∪[1,+∞)
的值域为(-∞,-1]∪[1,+∞)
∴若方程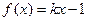 有实数
有实数 解,则实数
解,则实数 的取值范围是(
的取值范围是( -∞,-1]∪[1,+∞).
-∞,-1]∪[1,+∞).
解析

练习册系列答案
相关题目
已知 的值 ( )
的值 ( )
A.不大于 | B.大于 | C.不小于 | D.小于 |
 。
。 处的切线垂直y轴,求a的值;
处的切线垂直y轴,求a的值; ;
; ,
, ,求实数b的取值范围。
,求实数b的取值范围。
 的最小值;(2)若
的最小值;(2)若 在
在 内恒成立,求
内恒成立,求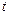 的取值范围
的取值范围 的图像在点
的图像在点 处
处 平行.
平行. 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
 .
.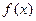 的极值;
的极值; 在
在 上恒成立,求
上恒成立,求 的取值范围;
的取值范围; ,且
,且 ,求证:
,求证: .
.
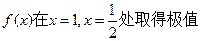 ,
, 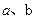 的值;
的值;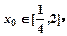 使得不等式
使得不等式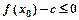 成立,求
成立,求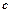 的最小值;
的最小值;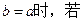
 上是单调函数,求
上是单调函数,求 的取值范围。
的取值范围。
 ________.
________.