题目内容
已知x∈（0，1]，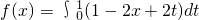
，则f（x）的值域是________．
[0，2）
分析：利用微积分基本定理先求出函数f（x）的解析式，再利用一次函数的单调性即可求出其值域．
解答：∵=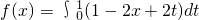
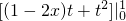=2-2x，即f（x）=-2x+2．
∵x∈（0，1]，∴f（1）≤f（x）＜f（0），即0≤f（x）＜2．
∴函数f（x）的值域是[0，2）．
故答案为[0，2）．
点评：熟练微积分基本定理和一次函数的单调性是解题的关键．
分析：利用微积分基本定理先求出函数f（x）的解析式，再利用一次函数的单调性即可求出其值域．
解答：∵
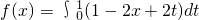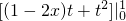==2-2x，即f（x）=-2x+2．∵x∈（0，1]，∴f（1）≤f（x）＜f（0），即0≤f（x）＜2．
∴函数f（x）的值域是[0，2）．
故答案为[0，2）．
点评：熟练微积分基本定理和一次函数的单调性是解题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
设f（x）是定义在R上以2为周期的偶函数，已知x∈（0，1）时，f（x）=log
（1-x），则函数f（x）在（1，2）上（ ）
| 1 |
| 2 |
| A、是减函数，且f（x）＞0 |
| B、是增函数，且f（x）＞0 |
| C、是增函数，且f（x）＜0 |
| D、是减函数，且f（x）＜0 |