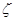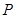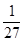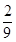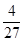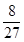题目内容
某射手每次射击击中目标的概率均为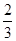
，且每次射击的结果互不影响
（I）假设这名射手射击3次，求至少2次击中目标的概率
（II）假设这名射手射击3次，每次击中目标10分，未击中目标得0分，在3次射击中，若有两次连续击中目标，而另外一次未击中目标，则额外加5分；若3次全部击中，则额外加10分。用随机变量§表示射手射击3次后的总得分，求§的分布列和数学期望。
【答案】
（I）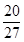
（II）故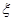
的分布列是
|
|
0 |
10 |
20 |
25 |
40 |
|
|
|
|
|
|
|
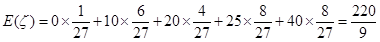
【解析】
试题分析：解：⑴设
为射手3次射击击中目标的总次数，则
.
故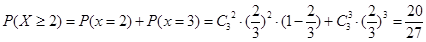
,
所以所求概率为.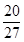
⑵由题意可知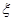，的所有可能取值为
,
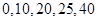用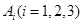
表示事件“第
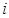次击中目标”，
则
，
，
，
，
.
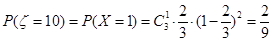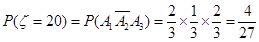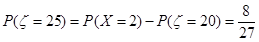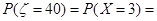
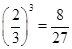故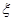的分布列是
|
|
0 |
10 |
20 |
25 |
40 |
|
|
|
|
|
|
|
.
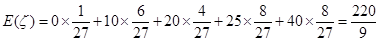考点：n次独立重复试验中恰好发生k次的概率；离散型随机变量的期望与方差．
点评：本题主要考查n次独立重复实验中恰好发生k次的概率，离散型随机变量的数学期望的求法，属于中档题．
练习册系列答案
相关题目