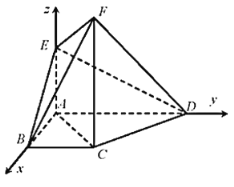
题目内容
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
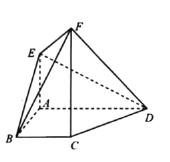
(1)求证:![]() ;
;
(2)若二面角![]() 是直二面角,求
是直二面角,求![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() ,证得
,证得![]() ,再由
,再由![]() ,得到
,得到![]() ,进而证得
,进而证得![]() 平面
平面![]() ,即可得到
,即可得到![]() ;
;
(2)以A为原点,![]() 、
、![]() 、
、![]() 分别为x轴、y轴、z轴正方向,建立空间直角坐标系,设
分别为x轴、y轴、z轴正方向,建立空间直角坐标系,设![]() ,分别求得平面
,分别求得平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,结合
,结合![]() ,求得
,求得![]() 的值,即可求解.
的值,即可求解.
(1)连接![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,可得
,可得![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,所以A,C,F,E四点共面,
,所以A,C,F,E四点共面,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)如图所示,以A为原点,![]() 、
、![]() 、
、![]() 分别为x轴、y轴、z轴正方向,
分别为x轴、y轴、z轴正方向,
建立空间直角坐标系,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,则
,则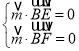 ,
,
即 ,取
,取![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则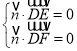 ,
,
即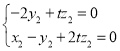 ,取
,取![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
由二面角![]() 是直二面角,则
是直二面角,则![]() ,即
,即![]() ,解得
,解得![]() .
.
所以![]() .
.

练习册系列答案
相关题目
【题目】万众瞩目的第14届全国冬季运动运会(简称“十四冬”)于2020年2月16日在呼伦贝尔市盛大开幕,期间正值我市学校放寒假,寒假结束后,某校工会对全校100名教职工在“十四冬”期间每天收看比赛转播的时间作了一次调查,得到如图频数分布直方图:
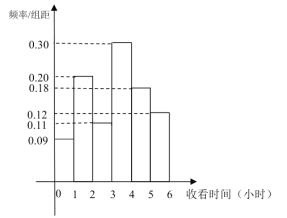
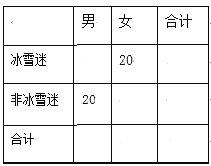
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“冰雪迷”,否则定义为“非冰雪迷”,请根据频率分布直方图补全![]() 列联表;并判断能否有
列联表;并判断能否有![]() 的把握认为该校教职工是否为“冰雪迷”与“性别”有关;
的把握认为该校教职工是否为“冰雪迷”与“性别”有关;
(2)在全校“冰雪迷”中按性别分层抽样抽取6名,再从这6名“冰雪迷”中选取2名作冰雪运动知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
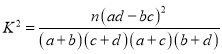 ,
,![]()