题目内容
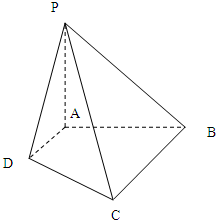 已知ABCD为直角梯形,AD∥BC,∠BAD=90°,AD=AB=1,BC=2,PA⊥平面ABCD,
已知ABCD为直角梯形,AD∥BC,∠BAD=90°,AD=AB=1,BC=2,PA⊥平面ABCD,(1)若异面直线PC与BD所成的角为θ,且cosθ=
| ||
| 6 |
(2)在(1)的条件下,设E为PC的中点,能否在BC上找到一点F,使EF⊥CD?
(3)在(2)的条件下,求二面角B-PC-D的大小.
分析:(1)以A为坐标原点,AD,AB,AP方向分别为x,y,z轴正方向建立空间坐标系,设|PA|=a,我们易求出异面直线PC与BD的方向向量的坐标,根据异面直线PC与BD所成的角为θ,且cosθ=
,构造关于a的方程,解方程即可求出|PA|的值;
(2)设F(x,1,0),我们分别求出直线EF和CD的方向向量,根据两直线垂直,两方向向量的数量积为0,构造关于x的方程,解方程求出x的值,即可找到满足条件的F点的位置.
(3)分别求出EF与PC的方向向量,根据其数量积为0,可得EF⊥PC,结合EF⊥CD由线面垂直的判定定理得EF⊥平面PCD,再由面面垂直的判定定理得平面PCB⊥平面PCD,由直二面角的定义可得二面角B-PC-D的大小.
| ||
| 6 |
(2)设F(x,1,0),我们分别求出直线EF和CD的方向向量,根据两直线垂直,两方向向量的数量积为0,构造关于x的方程,解方程求出x的值,即可找到满足条件的F点的位置.
(3)分别求出EF与PC的方向向量,根据其数量积为0,可得EF⊥PC,结合EF⊥CD由线面垂直的判定定理得EF⊥平面PCD,再由面面垂直的判定定理得平面PCB⊥平面PCD,由直二面角的定义可得二面角B-PC-D的大小.
解答:解:以A为坐标原点,AD,AB,AP方向分别为x,y,z轴正方向建立空间坐标系
(1)设|PA|=a,则P(0,0,a),C(2,1,0),B(0,1,0),D(1,0,0)
∴
=(2,1,-a),
=(1,-1,0)
由已知得:cosθ=
=
=
,即5+a2=6∴a=1(a>0)即|
=1|
(2)设能在BC上找到一点F,使EF⊥CD,设F(x,1,0),由(1)知P(1,0,0)∴E(1,
,
),
则
(x-1,
,-
),又有
=(-1,-1,0),∵EF⊥CD,∴
•
=x-1+
=0,
∴x=
,即存在点F(
,1,0)满足要求.
(3)∵
•
=(-
,
,-
)•(2,1,-1)=0
∴EF⊥PC;
∵EF⊥CD且PC∩CD=C∴EF⊥平面PCD.EF?平面,
所以平面PCB⊥平面PCD,故二面角B-PC-D的大小为90°.
(1)设|PA|=a,则P(0,0,a),C(2,1,0),B(0,1,0),D(1,0,0)
∴
| PC |
| BD |
由已知得:cosθ=
| ||||
|
|
| 1 | ||||
|
| ||
| 6 |
| PA |
(2)设能在BC上找到一点F,使EF⊥CD,设F(x,1,0),由(1)知P(1,0,0)∴E(1,
| 1 |
| 2 |
| 1 |
| 2 |
则
| EF= |
| 1 |
| 2 |
| 1 |
| 2 |
| CD |
| EF |
| CD |
| 1 |
| 2 |
∴x=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵
| EF |
| PC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EF⊥PC;
∵EF⊥CD且PC∩CD=C∴EF⊥平面PCD.EF?平面,
所以平面PCB⊥平面PCD,故二面角B-PC-D的大小为90°.
点评:本题考查的知识点是二面角的平面角及求法,异面直线及其所成的角,直线与平面垂直的性质,其中建立恰当的空间坐标系,求出相应直线的方向向量,将空间直线夹角问题,及直线的垂直问题,转化为向量夹角问题是解答本题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1, 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,