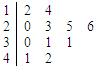题目内容
15.已知函数f(x)=$\frac{1}{3}$x3-(a-1)x2+b2x,其中a∈{1,2,3,4},b∈{1,2,3},则函数f(x)在R上是增函数的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 由导数易得函数单调递增需a-1≤b,列举可得总的基本事件数,易得符合题意的基本事件数,由概率公式可得.
解答 解:∵f(x)=$\frac{1}{3}$x3-(a-1)x2+b2x,
∴f′(x)=x2-2(a-1)x+b2,
要使函数f(x)在R上是增函数,需f′(x)=x2-2(a-1)x+b2≥0,
即△=4(a-1)2-4b2≤0,即a-1≤b,
∵a∈{1,2,3,4},b∈{1,2,3},
∴总的基本事件为(1,1),(1,2),(1,3),(2,1),(2,2),
(2,3),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3)共12个,
其中满足a-1≤b的有(1,1),(1,2),(1,3),(2,1),(2,2),
(2,3),(3,2),(3,3),(4,3)共9个,
∴所求概率为P=$\frac{9}{12}$=$\frac{3}{4}$
故选:D.
点评 本题考查列举法计算基本事件数及事件发生的概率,涉及函数的导数与单调性,属基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
6.已知f(x)=lnx-$\frac{x}{4}$+$\frac{3}{4x}$,g(x)=-x2-2ax+4,若对?x1∈(0,2],?x2∈[1,2],使得f(x1)≥g(x2)成立,则a的取值范围是( )
| A. | [-$\frac{1}{8}$,+∞) | B. | [$\frac{25-8ln2}{16}$,+∞) | C. | [-$\frac{1}{8}$,$\frac{5}{4}$] | D. | (-∞,$\frac{5}{4}$] |
10.执行如图的程序框图,若输入的a=209,b=76,则输出的a是( )


| A. | 3 | B. | 57 | C. | 19 | D. | 76 |
20.已知双曲线${x^2}-\frac{y^2}{2}=1$的焦点为F1、F2,点M在双曲线上且$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,则点M到x轴的距离为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
5.函数y=sinx的定义域为[a,b],值域为[-1,$\frac{1}{2}$],则b-a的最大值是( )
| A. | π | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | 2π |