题目内容
设计算法求| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |
分析:由已知中,程序的功能我们可以利用循环结构来解答本题,因为这是一个累加问题,故循环前累加器S=0,由于已知中的式子,可得循环变量k初值为1,步长为1,终值为99,累加量为
,由此易写出算法步骤,并画出程序框.
| 1 |
| k(k+1) |
解答:解:满足条件的算法步骤如下:
第一步,令s=0,k=1,
第二步,若k≤99成立,则执行第三步,否则输出s,结束算法;
第三步,s=s+
;
第四步,k=k+1,返回第二步.
满足条件的程序框图如下:
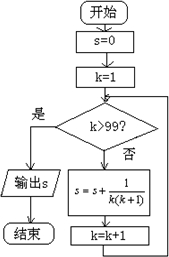
第一步,令s=0,k=1,
第二步,若k≤99成立,则执行第三步,否则输出s,结束算法;
第三步,s=s+
| 1 |
| k(k+1) |
第四步,k=k+1,返回第二步.
满足条件的程序框图如下:

点评:本题考查的知识点是程序框图解决实际问题,其中利用循环解答累加问题时,关键是根据已知中的程序确定循环变量的初值、步长、终值,及累加量的通项公式.

练习册系列答案
相关题目
 设计算法求
设计算法求