题目内容
 在极坐标系中,圆心在(
在极坐标系中,圆心在(| 2 |
分析:由题意画出极坐标系,画出以(
,0)为圆心,且过极点的圆,利用平面几何知识找到圆上任意一点的极径与极角的关系即可.
| 2 |
解答:解:如图,
设圆上任意一点的极坐标为P(ρ,θ),
∵圆心在(
,0),且圆过极点,
∴
=2
,即ρ=2
cosθ.
∴在极坐标系中,圆心在(
,0),且过极点的圆的方程为ρ=2
cosθ.
故选:D.
设圆上任意一点的极坐标为P(ρ,θ),
∵圆心在(
| 2 |
∴
| ρ |
| cosθ |
| 2 |
| 2 |
∴在极坐标系中,圆心在(
| 2 |
| 2 |
故选:D.
点评:本题考查了简单曲线的极坐标方程,解答的关键是利用已知条件找到极角和的关系,是基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
在极坐标系中,圆心在(
,π)且过极点的圆的方程为( )
| 2 |
A、ρ=2
| ||
B、ρ=-2
| ||
C、ρ=2
| ||
D、ρ=-2
|
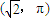 且过极点的圆的方程为 .
且过极点的圆的方程为 .