题目内容
(2014·广州模拟)已知☉M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切☉M于A,B两点.
(1)如果|AB|= ,求直线MQ的方程.
,求直线MQ的方程.
(2)求证:直线AB恒过一个定点.
(1)如果|AB|=
 ,求直线MQ的方程.
,求直线MQ的方程.(2)求证:直线AB恒过一个定点.
(1)2x+ y-2
y-2 =0或2x-
=0或2x- y+2
y+2 =0
=0
(2)见解析
 y-2
y-2 =0或2x-
=0或2x- y+2
y+2 =0
=0(2)见解析
(1)如图所示,连AM,BM,
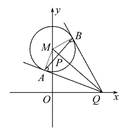
设P是AB的中点,由|AB|= ,
,
可得|MP|
=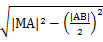
=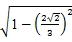 =
= .
.
由射影定理,得|MB|2=|MP|·|MQ|,得|MQ|=3,
在Rt△MOQ中,|OQ|=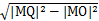 =
=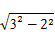 =
= ,
,
故Q点的坐标为( ,0)或(-
,0)或(- ,0),所以直线MQ的方程是:
,0),所以直线MQ的方程是:
2x+ y-2
y-2 =0或2x-
=0或2x- y+2
y+2 =0.
=0.
(2)设Q(a,0),由题意知M,A,Q,B四点共圆,直径为MQ.
设R(x,y)是该圆上任一点,由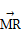 ·
·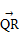 =0得x(x-a)+(y-2)y=0.
=0得x(x-a)+(y-2)y=0.
即x2+y2-ax-2y=0.①
①式与x2+(y-2)2=1联立,消去x2,y2项得两圆公共弦AB所在的直线方程为-ax+2y=3.
所以无论a取何值,直线AB恒过点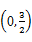 ,故直线AB恒过一个定点.
,故直线AB恒过一个定点.

设P是AB的中点,由|AB|=
 ,
,可得|MP|
=
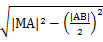
=
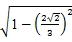 =
= .
.由射影定理,得|MB|2=|MP|·|MQ|,得|MQ|=3,
在Rt△MOQ中,|OQ|=
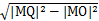 =
=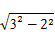 =
= ,
,故Q点的坐标为(
 ,0)或(-
,0)或(- ,0),所以直线MQ的方程是:
,0),所以直线MQ的方程是:2x+
 y-2
y-2 =0或2x-
=0或2x- y+2
y+2 =0.
=0.(2)设Q(a,0),由题意知M,A,Q,B四点共圆,直径为MQ.
设R(x,y)是该圆上任一点,由
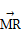 ·
·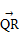 =0得x(x-a)+(y-2)y=0.
=0得x(x-a)+(y-2)y=0.即x2+y2-ax-2y=0.①
①式与x2+(y-2)2=1联立,消去x2,y2项得两圆公共弦AB所在的直线方程为-ax+2y=3.
所以无论a取何值,直线AB恒过点
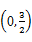 ,故直线AB恒过一个定点.
,故直线AB恒过一个定点.
练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
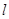 过圆
过圆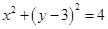 的圆心,且与直线
的圆心,且与直线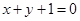 垂直,则
垂直,则



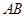 是圆
是圆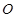 的直径,点
的直径,点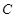 在圆
在圆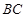 到
到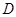 使
使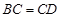 ,过
,过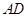 于
于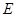 . 若
. 若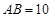 ,
, ,求
,求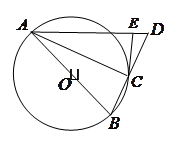
 与圆
与圆 有两个不同的交点,则点
有两个不同的交点,则点 圆C的位置关系是( )
圆C的位置关系是( )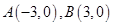 ,动点P 满足:|PA|=2|PB|.
,动点P 满足:|PA|=2|PB|.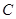 ,求此曲线的方程;
,求此曲线的方程;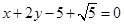 被圆
被圆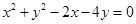 截得的弦长为
截得的弦长为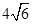
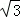 ,1),圆C:x2+y2=4,则直线l与圆C的位置关系是( )
,1),圆C:x2+y2=4,则直线l与圆C的位置关系是( )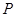 是函数
是函数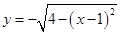 图象上的任意一点,点
图象上的任意一点,点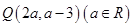 ,则
,则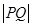 的最小值为( )
的最小值为( )


