题目内容
(本小题满分8分)已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、
黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)列出一次任取2个球的所有基本事件;
(3)从中取2个球,求至少有一个红球的概率.
【答案】
(1)从6只球中任取1球得红球有2种取法,得黑球有3种取法,得红球或黑球的共有2+3=5种不同取法,任取一球有6种取法,所以任取1球得红球或黑球的概率得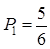 .
.
(2)将红球编号为红1,红2,黑球编号为黑1,黑2,黑3,则一次任取2个球的所有基本事件为:
红1红2 红1黑1 红1黑2 红1黑3 红1白
红2白 红2黑1 红2黑2 红2黑3 黑1黑2
黑1黑3 黑1白 黑2黑3 黑2白 黑3白
(3)由(2)知从6只球中任取两球一共有15种取法,其中至少有一个红球的取法共有9
种,所以其中至少有一个红球概率为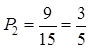 .
.
【解析】略

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 ,满足
,满足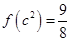
 的值;
的值;
 .
. ,集合A={
,集合A={ ,集合B=
,集合B=
 (2)
(2) 
 ,试确定
,试确定 的值,使得:
的值,使得: ;
(2)
;
(2) 
 ,
,  的夹角为
的夹角为 , 且
, 且 ,
,  ,
,  ; (2) 求
; (2) 求 .
.