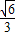题目内容

已知F1、F2是两个定点，点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点，并且PF1⊥PF2，e1和e2分别是上述椭圆和双曲线的离心率，则有

A.+=4                               B.+=2

C.e12+e22=4                                  D.e12+e22=2

【答案】B  设椭圆长轴长为2a1,双曲线实轴长为2a2,焦距均为2c,

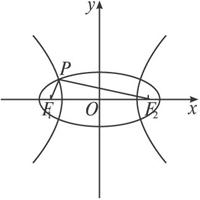
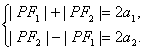∴∴|PF2|=a1+a2,|PF1|=a1-a2.

∵PF1与PF2垂直,∴|PF1|2+|PF2|2=|F1F2|2.

∴(a1+a2)2+(a1-a2)2=4c2,∴2a12+2a22=4c2.∴+=2.

练习册系列答案
相关题目
已知F1、F2是两个定点，点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点，并且PF1⊥PF2，e1和e2分别是上述椭圆和双曲线的离心率，则有（　　）
A、e12+e22=2
B、e12+e22=4
C、
1
e
2
1
+
1
e
2
2
=2
D、
1
e
2
1
+
1
e
2
2
=4
已知F1，F2是两个定点，椭圆C1和等轴双曲线C2都以F1，F2为焦点．点P是C1和C2的一个交点，且
PF1
•
PF2
=0，那么椭圆C1的离心率为（　　）
已知F1、F2是两个定点，点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点，并且PF1⊥PF2，e1和e2分别是上述椭圆和双曲线的离心率，则有（　　）
A．e12+e22=2B．e12+e22=4
C．
1
e21
+
1
e22
=2		D．
1
e21
+
1
e22
=4
已知F1，F2是两个定点，椭圆C1和等轴双曲线C2都以F1，F2为焦点．点P是C1和C2的一个交点，且，那么椭圆C1的离心率为（ ）
A．
B．
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网