Question

（13分）设为常数）。

（1）当时，证明：不是奇函数；

（2）设是奇函数，求与的值；

（3）当是奇函数时，研究是否存在这样的实数集的子集，对任何属于的、，都有成立？若存在试找出所有这样的；若不存在，请说明理由。

Answer 1

解析：（Ⅰ）举出反例即可．，，，

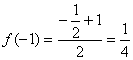所以，不是奇函数；……………4分

（Ⅱ）是奇函数时，，

即对定义域内任意实数成立．

化简整理得，这是关于的恒等式，

所以所以或 ．  经检验都符合题意．……………8分

(Ⅲ)（1）当时，，因为，所以，，从而；

而对任何实数成立；

所以可取=，对任何、c属于，都有成立．……10分

(2)当时，，

所以当时，；当时，；

1）因此取，对任何、c属于，都有成立．

2）当时，，解不等式得：．

所以取，对任何属于的、c，都有成立．………13分