Question

袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有一人取到白球时既终止，每个球在每一次被取出的机会是等可能的，用 ξ表示取球终止所需要的取球次数.

（1）求袋中所有的白球的个数；

（2）求随机变量ξ的概率分布；

（3）求甲取到白球的概率.

Answer 1

思路分析：（1）求袋中原有白球的个数，需设出白球的个数，利用古典概型公式，列出方程组求解;（2）写出ξ的可能取值，求出相应概率，写出ξ的分布列;（3）利用所求的分布列，甲取到白球的概率为P(A)=P(ξ=1)+P(ξ=3)+P(ξ=5).

解：(1)设袋中原有n个白球,由题意知.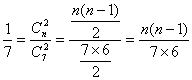

可得 n=3或n=-2(舍去),即袋中原有3个白球.

(2)由题意, ξ的可能取值为1,2,3,4,5.

P(ξ=1)=;P(ξ=2)=;P(ξ=3)=;

P(ξ=4)=;

P(ξ=5)=

所以ξ的分布列为

ξ	1	2	3	4	5
P

     (3)因为甲先取,所以甲只有可能在第一次,第三次和第五次取球,

记“甲取到白球”为事件A，则P（A）=P（ξ=1）+P(ξ=3)+P(ξ=5)=.

    深化升华 本题考查知识面广，包括等可能事件，互斥事件，随机变量的概率分布等知识，可以运用方程组的思想求出白球的个数.