题目内容
已知椭圆C以坐标轴为对称轴,以原点为对称中心,椭圆的一个焦点为(1,0),点 在椭圆上,直线l过椭圆的右焦点与椭圆交于M,N两点.
在椭圆上,直线l过椭圆的右焦点与椭圆交于M,N两点.(Ⅰ)求椭圆C的方程;
(Ⅱ)若线段MN的垂直平分线过点
 ,求出直线l的方程.
,求出直线l的方程.
【答案】分析:(Ⅰ)由题设条件知c=1,由点 在椭圆上,知b2=2,a2=3,由此能求出椭圆方程.
在椭圆上,知b2=2,a2=3,由此能求出椭圆方程.
(Ⅱ)当k不存在时,MN的垂直平分线为x轴,不过点 ,不合题意.设直线
,不合题意.设直线 ,(2+3k2)x2-6k2x+3k2-6=0,然后由韦达定理进行求解.
,(2+3k2)x2-6k2x+3k2-6=0,然后由韦达定理进行求解.
解答:解:(Ⅰ)设椭圆方程 ∵点
∵点 在椭圆上,
在椭圆上,
∴ 分∴
分∴ 分
分
(Ⅱ)当k不存在时,MN的垂直平分线为x轴,不过点 ,不合题意.…(7分)
,不合题意.…(7分)
设直线 ∴(2+3k2)x2-6k2x+3k2-6=0…(8分)∴
∴(2+3k2)x2-6k2x+3k2-6=0…(8分)∴ ∴
∴ 分∴
分∴ ∴
∴ 分
分
点评:本题考查椭圆方程的求法和直线与椭圆的位置关系的应用,解题时要认真审题,注意合理地进行等价转化.
 在椭圆上,知b2=2,a2=3,由此能求出椭圆方程.
在椭圆上,知b2=2,a2=3,由此能求出椭圆方程.(Ⅱ)当k不存在时,MN的垂直平分线为x轴,不过点
 ,不合题意.设直线
,不合题意.设直线 ,(2+3k2)x2-6k2x+3k2-6=0,然后由韦达定理进行求解.
,(2+3k2)x2-6k2x+3k2-6=0,然后由韦达定理进行求解.解答:解:(Ⅰ)设椭圆方程
 ∵点
∵点 在椭圆上,
在椭圆上,∴
 分∴
分∴ 分
分(Ⅱ)当k不存在时,MN的垂直平分线为x轴,不过点
 ,不合题意.…(7分)
,不合题意.…(7分)设直线
 ∴(2+3k2)x2-6k2x+3k2-6=0…(8分)∴
∴(2+3k2)x2-6k2x+3k2-6=0…(8分)∴ ∴
∴ 分∴
分∴ ∴
∴ 分
分点评:本题考查椭圆方程的求法和直线与椭圆的位置关系的应用,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
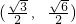 在椭圆上,直线l过椭圆的右焦点与椭圆交于M,N两点.
在椭圆上,直线l过椭圆的右焦点与椭圆交于M,N两点.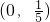 ,求出直线l的方程.
,求出直线l的方程.